卷积神经网络

\[ \begin{align}\begin{aligned}\newcommand{\ba}{\boldsymbol{a}} \newcommand{\bb}{\boldsymbol{b}} \newcommand{\be}{\boldsymbol{e}} \newcommand{\bw}{\boldsymbol{w}} \newcommand{\bx}{\boldsymbol{x}} \newcommand{\by}{\boldsymbol{y}} \newcommand{\bz}{\boldsymbol{z}} \newcommand{\bd}{\boldsymbol{d}} \newcommand{\bv}{\boldsymbol{v}} \newcommand{\bs}{\boldsymbol{s}}\\\newcommand{\btheta}{\boldsymbol{\theta}} \newcommand{\bbeta}{\boldsymbol{\beta}} \newcommand{\bgamma}{\boldsymbol{\gamma}} \newcommand{\bsigma}{\boldsymbol{\sigma}} \newcommand{\md}{\mbox{d}} \newcommand{\bmu}{\boldsymbol{\mu}} \newcommand{\bone}{\boldsymbol{1}} \newcommand{\trans}{^{\rm\scriptsize T}} \newcommand{\var}{\mathrm{var}}\\\newcommand{\bA}{\boldsymbol{A}} \newcommand{\bB}{\boldsymbol{B}} \newcommand{\bC}{\boldsymbol{C}} \newcommand{\bD}{\boldsymbol{D}} \newcommand{\bI}{\boldsymbol{I}} \newcommand{\bM}{\boldsymbol{M}} \newcommand{\bW}{\boldsymbol{W}} \newcommand{\bX}{\boldsymbol{X}} \newcommand{\bY}{\boldsymbol{Y}} \newcommand{\bZ}{\boldsymbol{Z}} \newcommand{\cotp}{\textcolor{ #30D158FF }{TP}} \newcommand{\cotn}{\textcolor{#64D2FFFF}{TN}} \newcommand{\cofp}{\textcolor{#5E5CE6FF}{FP}} \newcommand{\cofn}{\textcolor{#BF5AF2FF}{FN}}\\\newcommand{\numcotp}{\textcolor{ #30D158FF }{50}} \newcommand{\numcotn}{\textcolor{#64D2FFFF}{30}} \newcommand{\numcofp}{\textcolor{#5E5CE6FF}{10}} \newcommand{\numcofn}{\textcolor{#BF5AF2FF}{10}}\end{aligned}\end{align} \]

卷积神经网络#

\(\hspace{1.5em}\) 在之前的内容中，我们学习了神经网络的基本概念、全连接神经网络以及对神经网络模型的一些基本分析。在本章中，我们将学习卷积神经网络（Convolutional Neural Network, CNN）的基本概念、结构和应用。卷积神经网络是一种专门用于处理具有类似网格结构的数据的神经网络，例如图像数据。卷积神经网络在图像识别、图像分类、目标检测等领域取得了巨大的成功，是深度学习领域中最重要的模型之一。

\(\hspace{1.5em}\) 涉及到图像数据，一个自然的想法是，为什么不直接使用全连接神经网络来处理图像数据呢？我们完全可以把图像的每一个像素看作是一个特征，然后将图像展开成一个长向量，然后使用全连接神经网络来处理这个长向量。在 神经网络在干什么？以MNIST数据集为例 这一节中，我们也通过一个简单的全连接神经网络对MNIST数据集进行了分类，并且达到了相当高的准确率。但是，在处理更为复杂的图像数据时，全连接神经网络的缺点就显现出来了。总的来说，全连接神经网络在处理图像数据时存在以下不足：

  1. 参数量：对于一个大小为\(28\times28\)的图像，如果使用一个只有一个隐藏层的全连接神经网络，那么第一层的参数量就有\(784\times128=100352\)个，第二层的参数量就有\(128\times10=1280\)个，总共有\(101632\)个参数。实际应用中，彩色图像具有三个通道，并且分辨率也远远高于\(28\times28\)，因此参数量会更大，对内存要求极高。参数量过大会导致模型的训练变得非常缓慢，同时也容易导致过拟合。

  2. 空间结构： 图像具有重要的空间结构信息。相邻的像素在表示的含义上有很大的相关性。全连接神经网络会忽略图像的空间结构信息，而将图像展开成一个长向量，这样就会丢失这样的空间结构。

  3. 平移不变性：对于图像识别、语义分割等任务，对象在图像中的位置并不重要。但是全连接神经网络对不同位置的像素有截然不同的参数，这可能会导致相同含义的图片因为细微的差异，造成完全不同的输出。

\(\hspace{1.5em}\) 因此，对于图像数据的上述特征，有必要针对性的涉及网络结构，使网络天生具有提取图片特征、平移不变性等能力，能够用较少的参数量实现出色的效果。卷积神经网络就是为了解决这些问题而设计的。本章中，我们将首先介绍卷积的基本概念，然后介绍卷积神经网络的基本结构，之后我们会推导卷积神经网络的反向传播算法并实现一个简单的卷积神经网络，最后我们会介绍一些重要的卷积神经网络的变种。

卷积操作#

\(\hspace{1.5em}\) 在本小节中，我们将介绍卷积神经网络的核心组件——卷积操作。我们将先从一维卷积开始，介绍卷积、填充、步幅等重要概念，然后介绍二维卷积和多通道卷积。

事实上，卷积并非一个陌生的概念。在概率论与数理统计中，对于两个随机变量 \(X\) 和 \(Y\)，卷积是计算两个随机变量之和的概率分布的操作，我们令 \(Z=X+Y\)，则 \(Z\) 的概率分布为：

\[\begin{equation} f_Z(z) = \int_{-\infty}^{\infty} f_X(x)f_Y(z-x)\mu (dx). \end{equation}\]

其中 \(f_X(x)\) 和 \(f_Y(y)\) 分别为 \(X\) 和 \(Y\) 的概率密度函数，\(\mu\) 为测度。对于离散随机变量，卷积的计算公式为：

\[\begin{equation} f_Z(z) = \sum_{x} f_X(x)f_Y(z-x). \end{equation}\]

直观上来看，卷积是一种融合两个函数的操作，反映了两个随机变量之和的概率分布。而在信号处理、图像处理等领域，卷积是（Convolution）1由于图像在计算机中以离散的数值表示，在之后的内容中，我们只讨论离散序列的卷积。一种提取、强化信号特征的操作。我们将会在后面的内容中看到，不同的卷积核可以提取出不同的特征，从而实现图像的分类、识别等任务。

一维卷积#

\(\hspace{1.5em}\) 一维卷积常被用于信号处理中。假设我们有一个长度为 \(d\) 的序列 \(\boldsymbol{X}=(x_1,\ldots,x_d)\trans\)，以及一个长度为 \(f=3\) 的权重向量 \(\boldsymbol{W}=(w_1,w_2,w_3)\trans\)。我们可以通过将每个位置的元素与其周围的元素加权求和得到一个长度为 \(d-3+1=d-2\) 的序列 \(\boldsymbol{Z}=(z_1,\ldots,z_{d-2})\trans\)，其中对于 \(i=1, \ldots,d-2\)，\(z_i\) 的计算公式如下：

\[\begin{equation} z_i = w_1 x_{i} + w_2 x_{i+1} + w_3 x_{i+2}. \end{equation}\]

我们将权重向量 \(\boldsymbol{W}\) 称为卷积核（Convolution Kernel）或滤波器（Filter）。卷积核的大小决定了加权求和的范围，通常远小于输入序列的大小。下面这个视频展示了一个简单的1维卷积操作的过程：

在这个视频中，我们的原始序列为 \([3, 6, 5, 4, 8, 9, 1, 7, 9, 6]\)，卷积核为 \([-1, 0, 1]\)。在卷积操作中，我们将卷积核沿着原始序列滑动，每次计算卷积核与原始序列的加权求和。在序列最开始的位置，卷积核与原始序列的前三个元素（\([3, 6, 5]\)）进行加权求和，得到第一个卷积结果；然后卷积核向右移动一个元素，再次与原始序列的三个元素（\([6, 5, 4]\)）进行加权求和，得到第二个卷积结果；以此类推，直到卷积核滑动到序列的最后一个位置，得到最后一个卷积结果。如下所示

\[\begin{split}\begin{equation} \begin{array}{ccccr} z_1 &=& 3 \times (-1) + 6 \times 0 + 5 \times 1 &=& 2, \\ z_2 &=& 6 \times (-1) + 5 \times 0 + 4 \times 1 &=& -2, \\ &&…& \\ z_8 &=& 7 \times (-1) + 9 \times 0 + 6 \times 1 &=& -1. \end{array} \end{equation}\end{split}\]

最终，我们得到了一个长度为 \(d-3+1\) 的卷积结果序列。

\(\hspace{1.5em}\) 不同取值的卷积核可以获得不同的卷积效果。比如我们考虑一个大小为 \(f=3\) 的均值卷积核，其元素为 \(\boldsymbol{W}=(\frac{1}{3}, \frac{1}{3}, \frac{1}{3})\trans\)，这个卷积核相当于统计中的滑动窗口平均，可以平滑输入序列。如果我们考虑一个大小为 \(f=3\) 的边缘检测卷积核，其元素为 \(\boldsymbol{W}=(-1, 0, 1)\trans\)，这个卷积核可以检测输入序列中的边缘，我们实现一个简单的边缘检测卷积核来展示其效果：

 1import numpy as np
 2import matplotlib.pyplot as plt
 3
 4def conv1d(input_signal, kernel, stride=1, padding=0):
 5    """
 6    1D 卷积实现
 7    :param input_signal: 输入信号 (1D numpy array)
 8    :param kernel: 卷积核 (1D numpy array)
 9    :param stride: 步长 (int)
10    :param padding: 填充大小 (int)
11    :return: 卷积结果 (1D numpy array)
12    """
13    # 在输入信号两端添加零填充
14    input_signal = np.pad(input_signal, (padding, padding), mode='constant')
15    input_length = len(input_signal)
16    kernel_length = len(kernel)
17
18    # 计算输出信号长度
19    output_length = (input_length - kernel_length) // stride + 1
20    output_signal = np.zeros(output_length)
21
22    # 卷积计算
23    for i in range(output_length):
24        start = i * stride
25        end = start + kernel_length
26        output_signal[i] = np.sum(input_signal[start:end] * kernel)
27
28    return output_signal
29
30# 创建一个输入信号（阶跃信号）
31length = 50
32input_signal = np.zeros(length)
33input_signal[20:30] = 1  # 在20到30位置有一个高值区域
34
35# 定义卷积核（边缘检测）
36kernel = np.array([-1, 0, 1])  # 检测信号的变化
37
38# 应用卷积
39output_signal = conv1d(input_signal, kernel, stride=1, padding=1)
40
41# 绘制输入和输出信号
42plt.figure(figsize=(10, 5))
43
44plt.subplot(2, 1, 1)
45plt.plot(input_signal, label="Input Signal", drawstyle='steps-mid', linewidth=2)
46plt.title("输入信号（阶跃信号）")
47# plt.legend()
48
49plt.subplot(2, 1, 2)
50plt.plot(output_signal, label="Output Signal (After 1D Convolution)", color="orange", drawstyle='steps-mid', linewidth=2)
51plt.title("输出信号（边缘检测）")
52# plt.legend()
53plt.tight_layout()
54# plt.show()
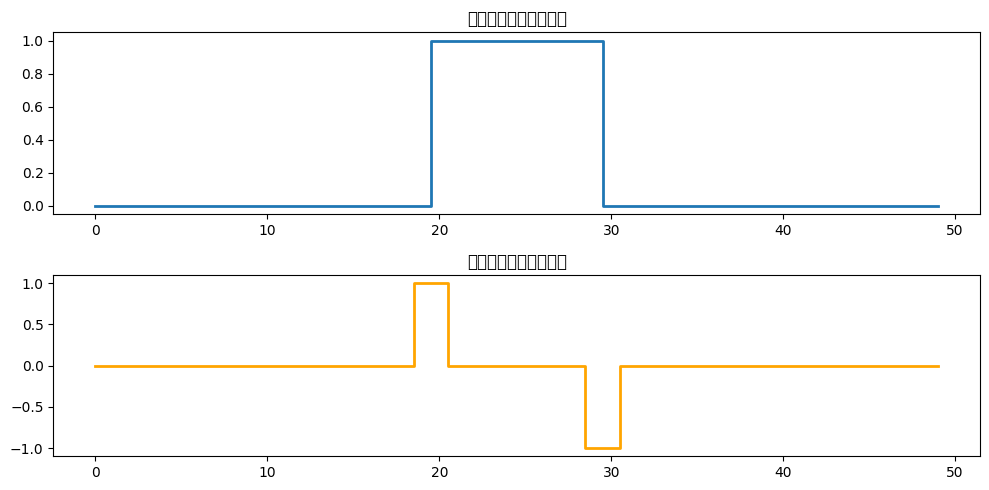
../_images/5_0_chapter_CNN_0_1.png

如图所示，我们在原始信号中10到20位置添加了一个高值区域，然后使用一个大小为3的边缘检测卷积核对输入信号进行卷积操作。在经过卷积操作之后，我们可以看到原始输入信号中由0到1的变化被检测出来，形成了一个大小为1的高值区域，而由1到0的变化也被检测出来，形成了一个大小为-1的低值区域。这个简单的边缘检测卷积核可以帮助我们检测输入信号中的边缘。

\(\hspace{1.5em}\) 在上面的代码中，注意到卷积操作会使输出序列的长度减小，因此我们在输入序列的两端添加了0值填充。在实际应用中，我们可以通过填充（Padding）的方式使输出序列长度与原始序列长度相同，或者使序列边界元素的利用率与中间元素相似。填充是在序列的两端添加一个或多个元素，填充的元素通常为0。例如，对于大小为 \(f=3\) 的卷积核，我们可以在序列的两端各填充一个元素。下面这个视频展示了一个添加了填充 \(p=1\) 的一维卷积操作的过程，其输入和输出序列长度相同：

\(\hspace{1.5em}\) 对于声音、高频信号等序列数据，由于序列元素密度较高，相邻元素之间的相关性较强，近距离的元素之间重叠的信息较多，此时我们可以通过调整步幅（Stride）来减少卷积操作的次数并减少输出序列的长度。步幅是卷积核每次移动的距离。例如，对于步幅为 \(s=2\) 的卷积操作，卷积核每次移动两个元素再执行一次卷积运算。下面这个视频展示了一个添加了步幅 \(s=2\) 的一维卷积操作的过程：

二维卷积#

\(\hspace{1.5em}\) 二维卷积是卷积神经网络中最常用的卷积操作。二维卷积的卷积核是一个矩阵，与一维卷积类似，卷积核在输入图像上由左到右、由上到下滑动。当卷积核在图像上滑动时，它会与图像中的局部区域进行元素乘法，然后将所有乘积的结果相加，生成一个新的像素值。这个过程在图像的每一个位置重复进行，最终生成一个新的图像，称为特征图（feature map）。具体来说，我们通常使用一个大小为 \(f\times f\) 的正方形卷积核 \(\bW=(w_{kl})\) 对一个大小为 \(d_H\times d_W\) 的“图像” \(\bX=(x_{ij})\) 进行卷积操作，进而得到一个 \((d_H-f+1)\times(d_W-f+1)\) 的“图像” \(\bZ=(z_{ij})\)。卷积操作的计算公式2严格来说，此处的卷积操作是互相关（Cross-Correlation）操作，而不是卷积（Convolution）操作。但在深度学习中，我们通常将互相关操作称为卷积操作。 如下：

\[\begin{equation} z_{ij} = \sum_{k=1}^{f}\sum_{l=1}^{f} x_{i+k-1, j+l-1} w_{kl}. \end{equation}\]

将其表示为矩阵形式如下：

\[\begin{equation} \boldsymbol{Z} = \bX \ast \bW. \end{equation}\]

其中 \(\ast\) 表示卷积运算。与一维卷积类似，我们可以通过填充和步幅来控制输出图像的大小。下面这个视频展示了一个填充 \(p=1\)、步幅 \(s=2\) 的二维卷积操作的过程：

\(\hspace{1.5em}\) 卷积核的不同参数会导致不同的卷积操作，从而提取不同的特征。例如，以下几个较为常见的卷积核：

\[\begin{split}\begin{equation} \boldsymbol{W}_1 = \begin{bmatrix} 1/9 & 1/9 & 1/9 \\ 1/9 & 1/9 & 1/9 \\ 1/9 & 1/9 & 1/9 \end{bmatrix} \quad \boldsymbol{W}_2 = \begin{bmatrix} 1/16 & 1/8 & 1/16 \\ 1/8 & 1/4 & 1/8 \\ 1/16 & 1/8 & 1/16 \end{bmatrix} \quad \boldsymbol{W}_3 = \begin{bmatrix} -1 & -1 & -1 \\ -1 & 9 & -1 \\ -1 & -1 & -1 \end{bmatrix} \quad \boldsymbol{W}_4 = \begin{bmatrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{bmatrix} \quad \boldsymbol{W}_5 = \begin{bmatrix} -1 & -2 & -1 \\ 0 & 0 & 0 \\ 1 & 2 & 1 \end{bmatrix} \end{equation}\end{split}\]

其中： 1. \(\boldsymbol{W}_1\) 是一个平滑均值卷积核，用于平滑图像。 2. \(\boldsymbol{W}_2\) 是一个高斯卷积核，更突出了中心点在像素平滑后的权重，相比于 \(\boldsymbol{W}_1\)，\(\boldsymbol{W}_2\) 的平滑效果好。 3. \(\boldsymbol{W}_3\) 是一个锐化卷积核，用于增强图像的边缘。 4. \(\boldsymbol{W}_4\) 和 \(\boldsymbol{W}_5\) 是两个Sobel卷积核，分别用于检测图像的垂直边缘和水平边缘。

\(\hspace{1.5em}\) 下图展示了这些卷积核的效果：

../_images/Figure_5_1_conv_kernel.png

图 12 卷积核的效果。为了更好的展示卷积核的效果，均值卷积核和高斯卷积核的大小为 \(5\times5\)，其余卷积核的大小仍为 \(3\times3\)。#

通过比较上图中展示的结果，我们可以得到如下结论。均值卷积核和高斯卷积核得到的图像相比于原图像边界更加模糊，锐化卷积核增强了图像的边缘，减弱了色块之间的过渡，Sobel卷积核分别检测了图像的垂直边缘和水平边缘。

\(\hspace{1.5em}\) 在卷积神经网络中，正是通过这些卷积核的不同参数，使得卷积神经网络能够提取图像的不同特征，从而实现图像的分类、识别等任务。在实际应用中，我们通常不会手动设计卷积核，而是通过训练的方式，使得卷积核能够自动学习到合适的参数。

多通道卷积#

\(\hspace{1.5em}\) 在上一节中，我们介绍了对于图像的二维卷积，但实际上，图像通常包含多个通道。例如，彩色图像包含RGB三个通道，每个通道都是一个独立的二维图像。在卷积操作中，我们可以为每个通道分别设置一个卷积核，然后将每个通道的卷积结果相加得到最终的输出。这种卷积操作称为多通道卷积。如下图所示

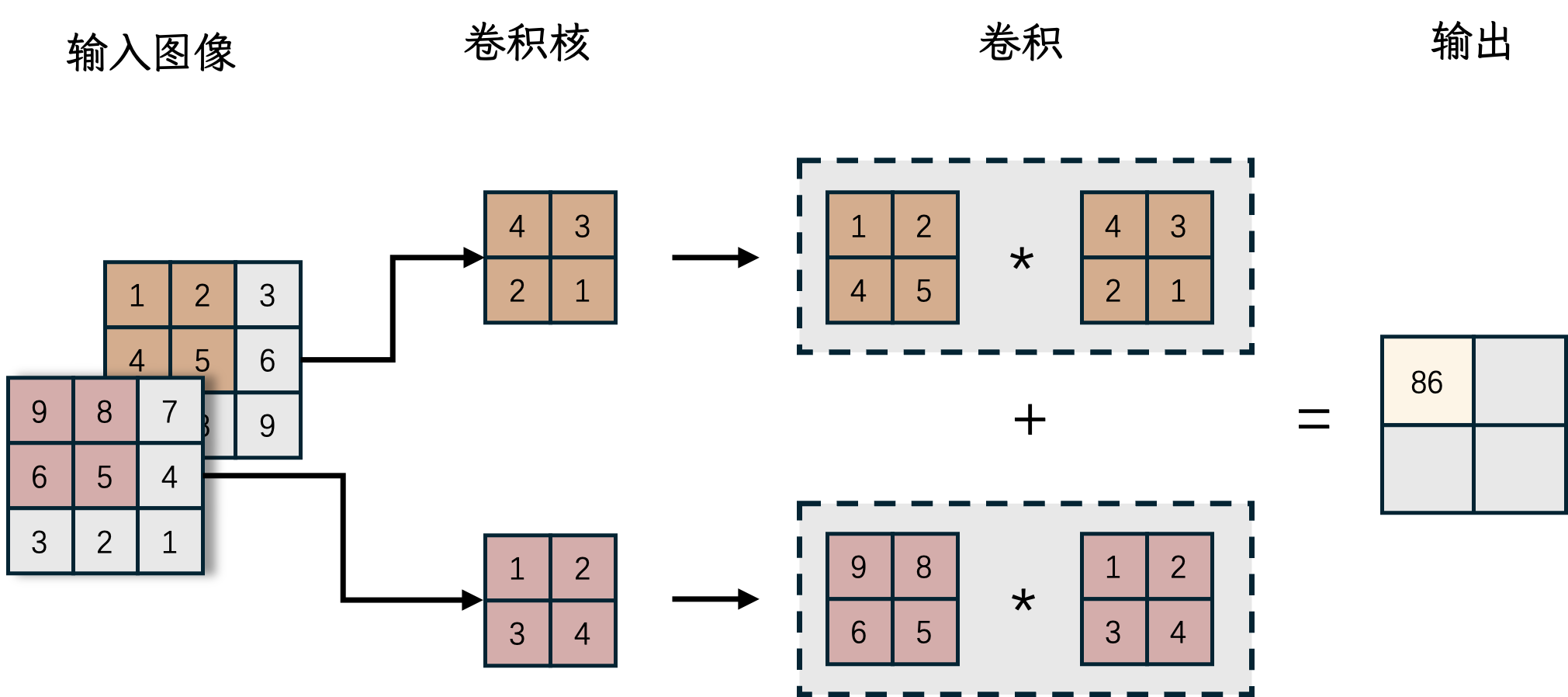
multi_channel

我们记输入图像的第 \(c\) 个通道对应的矩阵为 \(\boldsymbol{X}_{c}\)，第 \(c\) 个通道对应的卷积核为 \(\boldsymbol{W}_{c}\)。那么，多通道卷积的计算公式如下：

\[\begin{equation} \boldsymbol{Z} = \sum_{c=1}^{C} \boldsymbol{X}_{c} \ast \boldsymbol{W}_{c} \end{equation}\]

其中 \(C\) 为通道数。需要指出的是，在多通道卷积运算中，输入图像和卷积应当具有相同的通道数。

3D卷积

\(\hspace{1.5em}\) 请注意，多通道卷积与3D卷积（3D Convolution）是不同的概念。在三维卷积中，卷积核不仅在数据的宽度和高度上滑动，还在深度（或时间）维度上移动。这意味着卷积核本身也是三维的，它可以捕捉到数据在三个维度上的特征。在多通道卷积中，每个通道都有自己的卷积核，这些卷积核可以相同也可以不同。卷积操作在每个通道上独立进行，然后将所有通道的结果相加，生成一个单一的输出特征图。三维卷积是在三个空间（或时间）维度上进行的卷积，而多通道卷积是在多个特征通道上进行的二维卷积。

\(\hspace{1.5em}\) 下面这个视频展示了一个简单的多通道卷积操作的过程：

卷积神经网络#

\(\hspace{1.5em}\) 在上一节中，我们介绍了卷积的基本概念。在本节中，我们将介绍卷积神经网络（Convolutional Neural Network, CNN）的基本结构。一个基本的卷积神经网络通常包括若干个卷积层、池化层和全连接层。卷积层用于提取输入数据的特征，池化层用于减小输出维度，全连接层用于整合卷积层提取的特征。

\(\hspace{1.5em}\) 卷积层是卷积神经网络的核心部分。与全连接层不同，卷积层对输入数据的每个局部区域进行卷积运算并加上偏置，然后通过激活函数进行非线性变换后得到输出。考虑大小为 \(d_H\times d_W\) 的输入“图像” \(\bX=(x_{ij})\) ，以及大小为 \(f\times f\) 的卷积核 \(\bW=(w_{kl})\) 。我们令 Stride 为1， Padding 为0，卷积层的计算公式如下：

\[\begin{equation} z_{ij} = \sigma\left(\sum_{k=1}^{f}\sum_{l=1}^{f} x_{i+k-1, j+l-1} w_{kl}+ b\right), \end{equation}\]

其中 \(\bZ=(z_{ij})\) 为卷积计算结果，\(\sigma\) 是激活函数，\(b\) 是偏置，括号中的第一项是上节所介绍的卷积运算。需要指出的是，在得到卷积结果 \(\bZ\) 时，我们运用的是一个公共的偏置。用矩阵表示，卷积层的计算公式如下：

(39)#\[\begin{equation} \boldsymbol{Z} = \sigma(\boldsymbol{X} \ast \boldsymbol{W} +{b}), \end{equation}\]

其中 \(\ast\) 表示卷积运算，\(\boldsymbol{W}\) 是卷积核。在 () 中，我们运用了 numpy 的 广播机制 进行关于偏置的计算。 计算卷积层的参数包括卷积核和偏置，因此卷积层的参数数量为 \(f\times f + 1\) 。这个参数量级与输入图像的维度并无直接关系。对比与全连接神经网络模型，当输入图像规模很大时，卷积层的参数数量远小于全连接层的参数数量。

\(\hspace{1.5em}\) 与一层全连接层有多个神经元类似，一个卷积层通常也包含多个卷积核，分别提取图像的不同信息。需要指出的是，每个卷积核对应着一个偏置项。每个卷积核对输入数据进行卷积运算，然后通过激活函数进行非线性变换后得到输出。在下图中，我们运用 \(K\) 个卷积核进行信息提取：

conv_layer

\(\hspace{1.5em}\) 下面这个视频演示了多个卷积核同时对一个输入进行卷积，提取不同特征的过程：

\(\hspace{1.5em}\) 回到本章开头的问题，卷积层的两个重要性质充分减少了参数数量，并且使得卷积神经网络对平移具有不变性。这两个性质分别是：

  1. 局部连接：卷积层计算结果中的每个值只与输入图像数据的一个局部区域相连，因此我们可以通过一个维度小得多的卷积核来替代全连接层的大型权重矩阵。

  2. 参数共享：卷积层计算结果对于输入数据的每个局部区域使用相同的卷积核，减少了参数数量。此外，由于所有局部区域使用的是相同的卷积核，因此无论目标对象在图像中的位置如何，卷积层都可以有效的提取出目标对象的特征。

\(\hspace{1.5em}\) 但是，尽管卷积层的参数数量大大减少，卷积层的输出维度仍然可能很大。具体地讲，对于大小为 \(d_H\times d_W\) 的输入数据，大小为 \(f\times f\) 的卷积核， Stride 为 \(s\) ， Padding 为 \(p\) ，卷积层的输出维度为：

(40)#\[\begin{equation} \left\lfloor\frac{d_H-f+2p}{s}+1\right\rfloor \times \left\lfloor\frac{d_W-f+2p}{s}+1\right\rfloor， \end{equation}\]

其中 \(\lfloor\cdot\rfloor\) 表示向下取整。由于通常卷积核的维度以及 Stride 的大小并不会很大，因此卷积层的输出维度仍然保持在一个相当大的规模。如果在卷积层之后直接连接全连接层，全连接层的参数数量将会非常庞大，容易导致过拟合。因此，我们通常会在卷积层之后添加池化层来减小输出维度。

下采样

\(\hspace{1.5em}\) 一般将减小维度的操作称为“下采样”，而将增加维度的操作称为“上采样”。设置池化层、增加 Stride 等操作都可以减小输出维度，因此都可以看作是下采样操作。

\(\hspace{1.5em}\) 池化层（Pooling Layer）是卷积神经网络的另一个重要组成部分。池化层的作用是通过对输入数据的局部区域进行池化操作，减小输出维度。假设输入池化层的数据为 \(\bX\) ，大小为 \(d_H\times d_W\) ，可以将输入数据划分为若干个大小为 \(f\times f\) 的局部区域，这些局部区域之间允许有重叠。请注意，与卷积核类似，此处我们仍然用 \(f\) 表示局部区域大小。池化操作是对每个局部区域的数值进行某种统计操作，例如最大值、平均值等。常见的池化操作是最大池化（Max Pooling）和平均池化（Average Pooling）。对应于池化过程，我们通常令 Stride 为 \(s=f\)，Padding 为 \(p=0\)。记输出结果为 \(\bZ=(z_{ij})\)，其规模可通过 () 计算得到。下面我们讲介绍两种池化的计算过程。

\(\hspace{1.5em}\) 最大池化是对每个局部区域取最大值，计算公式如下：

\[\begin{equation} z_{ij} = \max_{k=1}^{f}\max_{l=1}^{f} x_{i+k-1, j+l-1} \end{equation}\]

\(\hspace{1.5em}\) 平均池化是对每个局部区域取平均值，计算公式如下：

\[\begin{equation} z_{ij} = \frac{1}{f^2}\sum_{k=1}^{f}\sum_{l=1}^{f} x_{i+k-1, j+l-1} \end{equation}\]

\(\hspace{1.5em}\) 下面这个视频展示了最大池化和平均池化的过程：

\(\hspace{1.5em}\) 池化层的参数数量为0，因此池化层不会增加模型的参数数量。池化层的主要作用是减小输出维度，从而减少全连接层的参数数量，防止过拟合。另外，池化层是对每个局部区域的特征进行某种程度的不变性操作，使得模型对于输入数据的微小变化具有稳健性。同时，池化层也是对局部区域特征的浓缩，使得模型更加关注图像的全局特征。

\(\hspace{1.5em}\) 一个最典型的卷积神经网络通常包括若干个卷积层、池化层和全连接层。卷积神经网络的结构通常如下：

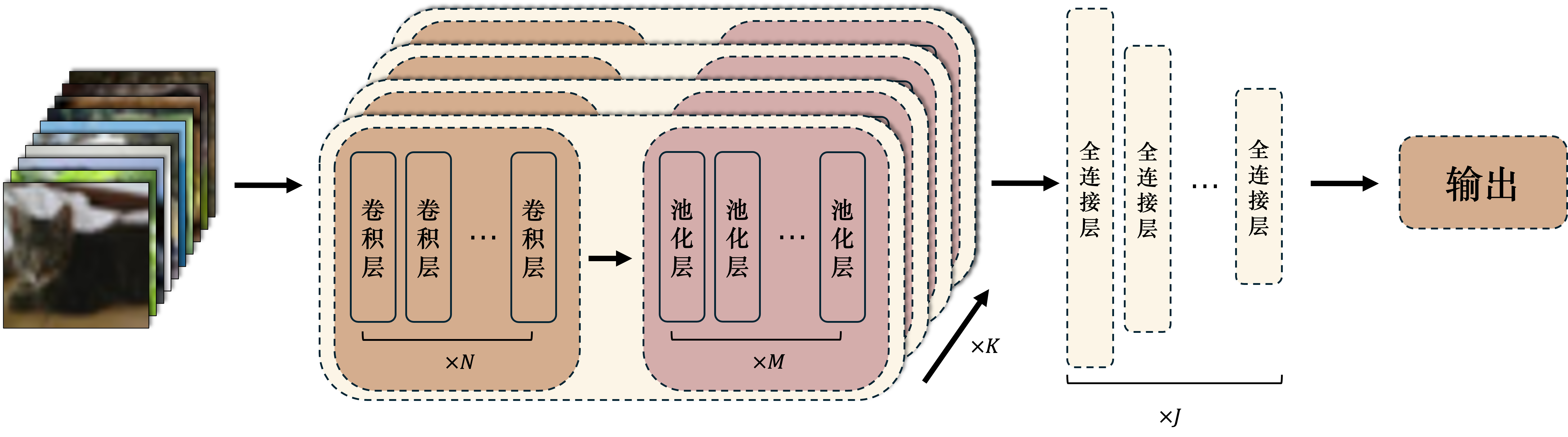cnn_arch 3注意与上文多个卷积核同时对一个输入进行卷积不同，这里的卷积层是顺序排列的，每个卷积层的输出作为下一个卷积层的输入。

图 13 卷积神经网络的基本结构3注意与上文多个卷积核同时对一个输入进行卷积不同，这里的卷积层是顺序排列的，每个卷积层的输出作为下一个卷积层的输入。。#

  1. 卷积模块：卷积模块由若干个卷积层和池化层组成。卷积层用于提取输入数据的特征，池化层用于减小输出维度。卷积模块的输出是一个高维特征图，包含了输入数据的局部特征。一般的卷积神经网络会包含多个卷积模块，每个卷积模块的输出作为下一个卷积模块的输入。

  2. 全连接模块：全连接模块由若干个全连接层组成。全连接层一方面用于整合卷积模块提取的特征，为神经网络提供更强的非线性表达能力；另一方面，全连接层可以看作是神经网络的“记忆”模块，保存着神经网络从训练数据中学到的知识。

\(\hspace{1.5em}\) 在后面的章节中，我们会更为具体的介绍一些经典的卷积神经网络结构，例如LeNet、AlexNet、VGG、GoogLeNet、ResNet等。这些卷积神经网络结构在图像分类、目标检测、语义分割等任务中取得了非常好的效果，是深度学习领域的重要里程碑。在这之前，让我们先学习一下卷积神经网络的反向传播。

卷积神经网络的参数学习#

\(\hspace{1.5em}\) 在这一节中，我们将讨论卷积神经网络的后向传播算法。上节中，我们了解了卷积神经网络具有卷积层、池化层和全连接层。全连接层的后向传播算法我们已经在之前的章节中讨论，这一节我们将主要讨论卷积层和池化层的参数学习与后向传播算法。

卷积层的参数学习与后向传播#

\(\hspace{1.5em}\) 假设第 \(l\) 层为卷积层，我们令卷积层的输入特征图为 \(\boldsymbol{X}^{(l-1)}\in\mathbb{R}^{H\times W\times C}\)，其中 \(H\) 为特征图的高度，\(W\) 为特征图的宽度，\(C\) 为特征图的通道数。卷积层的线性输出特征图为 \(\boldsymbol{Z}\in\mathbb{R}^{H'\times W'\times C'}\)，其中 \(H'\) 为输出特征图的高度，\(W'\) 为输出特征图的宽度，\(C'\) 为输出特征图的通道数。那么我们有：

\[\begin{align} \boldsymbol{Z}^{(l,c^{\prime})} &= \sum_{i=1}^{C}\boldsymbol{W}^{(l,c^{\prime},i)}\ast \boldsymbol{X}^{(l-1,i)} + b^{(l, c^{\prime})} , \end{align}\]

其中，\(\boldsymbol{W}^{(l,c^{\prime},i)}\in\mathbb{R}^{k\times k}\) 为第 \(l\) 层的第 \(c^{\prime}\) 个通道的第 \(i\) 个卷积核，\(\boldsymbol{X}^{(l-1,i)}\in\mathbb{R}^{H\times W}\) 为第 \(l-1\) 层的第 \(i\) 个通道的特征图，\(b^{(l, c^{\prime})}\) 为第 \(l\) 层的第 \(c^{\prime}\) 个通道的偏置项。

\(\hspace{1.5em}\) 根据链式法则，我们可以考虑一个抽象的损失函数 \(\mathcal{L}\)，以及该损失函数对于卷积层的输出特征图 \(\boldsymbol{Z}^{(l,c^{\prime})}\) 的梯度 \(\frac{\partial \mathcal{L}}{\partial \boldsymbol{Z}^{(l,c^{\prime})}}\)。我们希望计算损失函数对于卷积核 \(\boldsymbol{W}^{(l,c^{\prime},i)}\) 的梯度 \(\frac{\partial \mathcal{L}}{\partial \boldsymbol{W}^{(l,c^{\prime},i)}}\) 和损失函数对于卷积层的偏置项 \(b^{(l, c^{\prime})}\) 的梯度 \(\frac{\partial \mathcal{L}}{\partial b^{(l, c^{\prime})}}\), 我们有：

\[\begin{split}\begin{align} \frac{\partial \mathcal{L}}{\partial \boldsymbol{W}^{(l,c^{\prime},i)}} &= \frac{\partial \mathcal{L}}{\partial \boldsymbol{Z}^{(l,c^{\prime})}} \ast \boldsymbol{X}^{(l-1,i)} \\ \frac{\partial \mathcal{L}}{\partial b^{(l, c^{\prime})}} &= \sum_{m=1}^{H'}\sum_{n=1}^{W'}\frac{\partial \mathcal{L}}{\partial \boldsymbol{Z}^{(l,c^{\prime})}_{m,n}}, \end{align}\end{split}\]

\(\hspace{1.5em}\) 因此，只需要知道损失函数对于卷积层的输出特征图的梯度 \(\frac{\partial \mathcal{L}}{\partial \boldsymbol{Z}^{(l,c^{\prime})}}\)，我们就可以计算损失函数对于卷积核 \(\boldsymbol{W}^{(l,c^{\prime},i)}\) 和偏置项 \(b^{(l, c^{\prime})}\) 的梯度。我们可以通过后向传播算法计算损失函数对于卷积层的输出特征图的梯度 \(\frac{\partial \mathcal{L}}{\partial \boldsymbol{Z}^{(l,c^{\prime})}}\)，然后通过上面的公式计算损失函数对于卷积核和偏置项的梯度。

\(\hspace{1.5em}\) 在理清卷积层中参数的学习方法之后，我们还需要考虑在卷积层中梯度是如何传播到上一层的。我们令第 \(l-1\) 层的输出 \(\boldsymbol{X}^{(l-1, i)}\) 在经过激活函数 \(\sigma_{l-1}\) 之前的线性输出为 \(\boldsymbol{Z}^{(l-1,i)}\in\mathbb{R}^{H\times W\times C}\)，实际上，我们可以证明

\[\begin{split}\begin{align} \frac{\partial \mathcal{L}}{\partial \boldsymbol{Z}^{(l-1,i)}} &= \frac{\partial \boldsymbol{X}^{(l-1,i)}}{\partial \boldsymbol{Z}^{(l-1,i)}}\ast \frac{\partial \mathcal{L}}{\partial \boldsymbol{X}^{(l-1,i)}} \\ &= \sigma_{l-1}^{\prime}(\boldsymbol{Z}^{(l-1,i)}) \odot \sum_{c^{\prime}=1}^{C^{\prime}}\left(\text{rot180}(\boldsymbol{W}^{(l,c^{\prime},i)})\ast \frac{\partial \mathcal{L}}{\partial \boldsymbol{Z}^{(l,c^{\prime})}}\right), \end{align}\end{split}\]

其中，\(\odot\) 表示逐元素相乘，\(\text{rot180}\) 表示对卷积核进行旋转180度。

池化层的后向传播#

\(\hspace{1.5em}\) 由于池化层没有参数，因此我们只需要考虑损失函数对于池化层的输出特征图的梯度 \(\frac{\partial \mathcal{L}}{\partial \boldsymbol{Z}^{(l,c^{\prime})}}\) 如何传播到上一层。同样，我们令第 \(l-1\) 层的第 \(i\) 个通道的输出为 \(\boldsymbol{X}^{(l-1, i)}\in\mathbb{R}^{H\times W\times C}\)，在经过激活函数 \(\sigma_{l-1}\) 之前的输出为 \(\boldsymbol{Z}^{(l-1, i)}\in\mathbb{R}^{H\times W\times C}\)，我们有

\[\begin{split}\begin{align} \frac{\partial \mathcal{L}}{\partial \boldsymbol{Z}^{(l-1,i)}} &= \frac{\partial \boldsymbol{X}^{(l-1,i)}}{\partial \boldsymbol{Z}^{(l-1,i)}} \frac{\partial \mathcal{L}}{\partial \boldsymbol{X}^{(l-1,i)}} \\ &= \sigma_{l-1}^{\prime}(\boldsymbol{Z}^{(l-1,i)}) \odot \text{unpool}\left(\frac{\partial \mathcal{L}}{\partial \boldsymbol{Z}^{(l,i)}}\right), \end{align}\end{split}\]

\(\hspace{1.5em}\) 其中，\(\text{unpool}\) 表示上采样操作，与池化层的下采样操作相反。具体来说，如果池化层的下采样操作是 最大池化，那么上采样操作就是将上一层的特征图中的最大值放到池化层输出特征图中的对应位置，其他位置填充为0。如果池化层的下采样操作是 平均池化，那么上采样操作就是将上一层的特征图中的值均匀分配到池化层输出特征图中的对应位置。

几种经典的卷积神经网络#

\(\hspace{1.5em}\) 之前几节中，我们学习了卷积神经网络的一些基本组件、结构。在本小节中，我们将介绍几种经典的卷积神经网络，包括LeNet-5、AlexNet、VGG、MobileNet、Yolo和ResNet。这些网络在各自的提出时间点都具有非常重要的意义，是卷积神经网络发展的重要里程碑。这些网络的结构复杂度逐渐增加，性能也逐渐提高，为深度学习的发展提供了重要的参考。

LeNet-5#

\(\hspace{1.5em}\) LeNet-5 是一种经典的卷积神经网络架构，由 Yann LeCun 等人在 1998 年提出，主要用于手写数字识别（例如 MNIST 数据集）。它是最早的深度学习模型之一，它提出了卷积层、池化层和全连接层的组合，这种架构成为了后续CNN模型的基础。

LeNet-5 的网络结构如下所示：

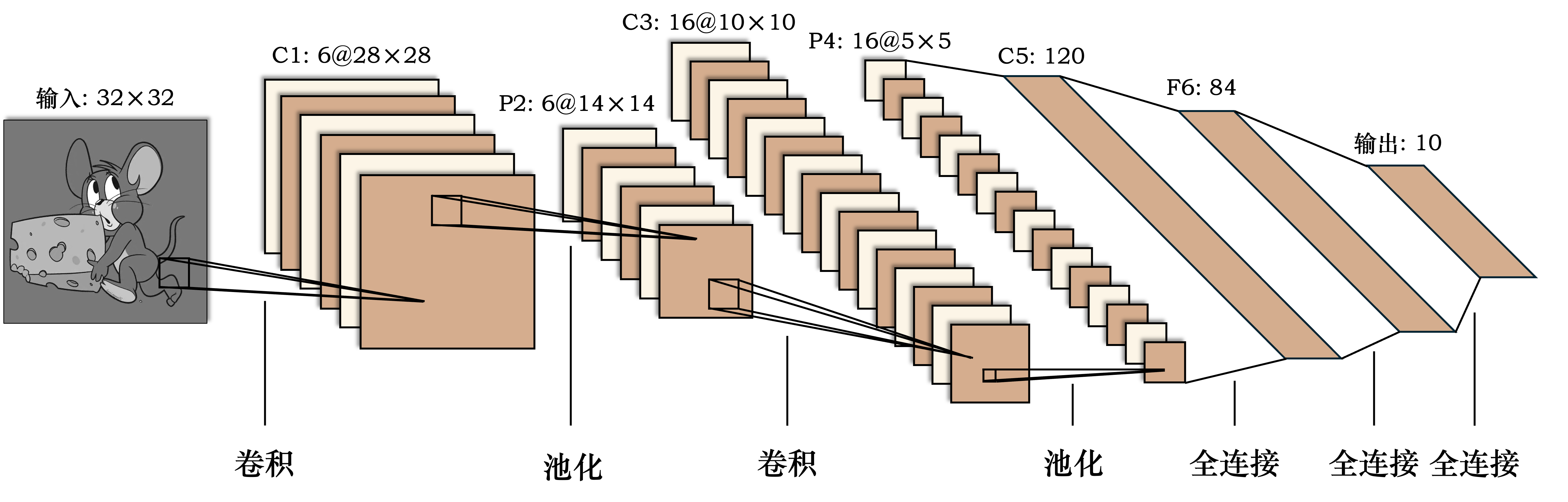
LeNet_arc

图 14 LeNet-5 的网络结构#

  1. 输入层

    • 输入：LeNet接收大小为32x32像素的灰度图像。

  2. 卷积层C1

    • 卷积核：6个5x5的卷积核，Stride=1，Padding=0。

    • 输出：6个28x28的特征图。

  3. 池化层S2

    • 池化类型：平均池化，池化窗口为2x2，Stride=2。

    • 输出：6个14x14的特征图。

  4. 卷积层C3

    • 卷积核：16个5x5的卷积核，Stride=1，Padding=0。

    • 输出：16个10x10的特征图。

  5. 池化层S4

    • 池化类型：平均池化，池化窗口为2x2，Stride=2。

    • 输出：16个5x5的特征图。

  6. 卷积层C5

    • 卷积核：120个5x5的卷积核，Stride=1，Padding=0。

    • 输出：120个1x1的特征图。

    • 说明：这个层的输出是120个值，每个值对应一个卷积核的输出。由于输入图像的大小和卷积核的大小相同，因此输出尺寸为1x1。这实际上等价于一个全连接层。

  7. 全连接层F6

    • 神经元数量：84。

    • 说明：这个层连接了C5层的输出，并将其展平成一个向量。84是一个经验选择的数字，类似于传统神经网络中的隐藏层。

  8. 输出层

    • 神经元数量：10。

\(\hspace{1.5em}\) 在经典的LeNet-5中，激活函数使用的是Sigmoid函数。在现代的实现中，Sigmoid函数通常被更加简单且效果更好的ReLU函数所替代。我们将在下一节中实现LeNet-5模型，并使用 torch 对 MNIST 数据集 进行分类。

AlexNet#

\(\hspace{1.5em}\) 尽管LeNet-5是第一个成功的卷积神经网络，但是它的规模相对较小，因此在更大的数据集上的表现并不理想。在实际的计算机视觉任务中，往往还是通过传统的特征提取方法（例如SIFT、HOG等）结合传统的分类器（例如SVM、KNN等）来完成。直到2012年，AlexNet的出现才真正将卷积神经网络推向了大众视野。AlexNet由Alex Krizhevsky等人在2012年的ImageNet大规模视觉识别挑战赛（ILSVRC）中取得了惊人的成绩，将Top-5错误率降低到了16.4%，远超第二名的26.2%。AlexNet的成功首次证明了，卷积神经网络提取特征的能力可以超过传统的特征提取方法。

\(\hspace{1.5em}\) 由于当时GPU计算能力的限制，AlexNet将网络分成两部分分别运行在两个GPU上。在这里，我们将AlexNet的网络结构整合到一个网络中，以便更好地展示。与LeNet-5相比，AlexNet的网络结构更加复杂，包含了更多的卷积层和全连接层。AlexNet的网络结构如下所示：

AlexNet_arc

图 15 AlexNet的网络结构（左：LeNet-5，右：AlexNet）#

\(\hspace{1.5em}\) 不仅在结构上有所改进，AlexNet还引入了一些新的技术，例如：

  1. 局部响应归一化 (LRN)：引入了一种新的正则化方法——局部响应归一化，用于增强模型的泛化能力和稳定性。LRN在卷积神经网络中可以帮助抑制弱激活，突出强激活。

  2. 池化层 (Pooling)：使用了最大池化层（max pooling），减少了参数的数量并降低了计算复杂度，同时保持了特征的不变性。

  3. Dropout：为了减少过拟合，AlexNet 在全连接层中引入了 Dropout 技术，以随机的方式忽略部分神经元的输出，减少了神经元间的相互依赖。

  4. 数据增强：使用了数据增强技术，通过对训练图像进行随机裁剪、翻转、颜色变化等操作，扩充了训练数据集，提高了模型的泛化能力。

\(\hspace{1.5em}\) 我们将在下一节中实现AlexNet模型，并用其对CIFAR-10数据集进行分类。

VGG#

\(\hspace{1.5em}\) VGG（Visual Geometry Group）网络是由牛津大学视觉几何组在2014年提出的一种深度卷积神经网络架构。VGG的重要地位在于其提出了“块”的概念，即将网络分成若干个块，每个块包含若干个卷积层和池化层。VGG块与VGG网络的结构如下所示：

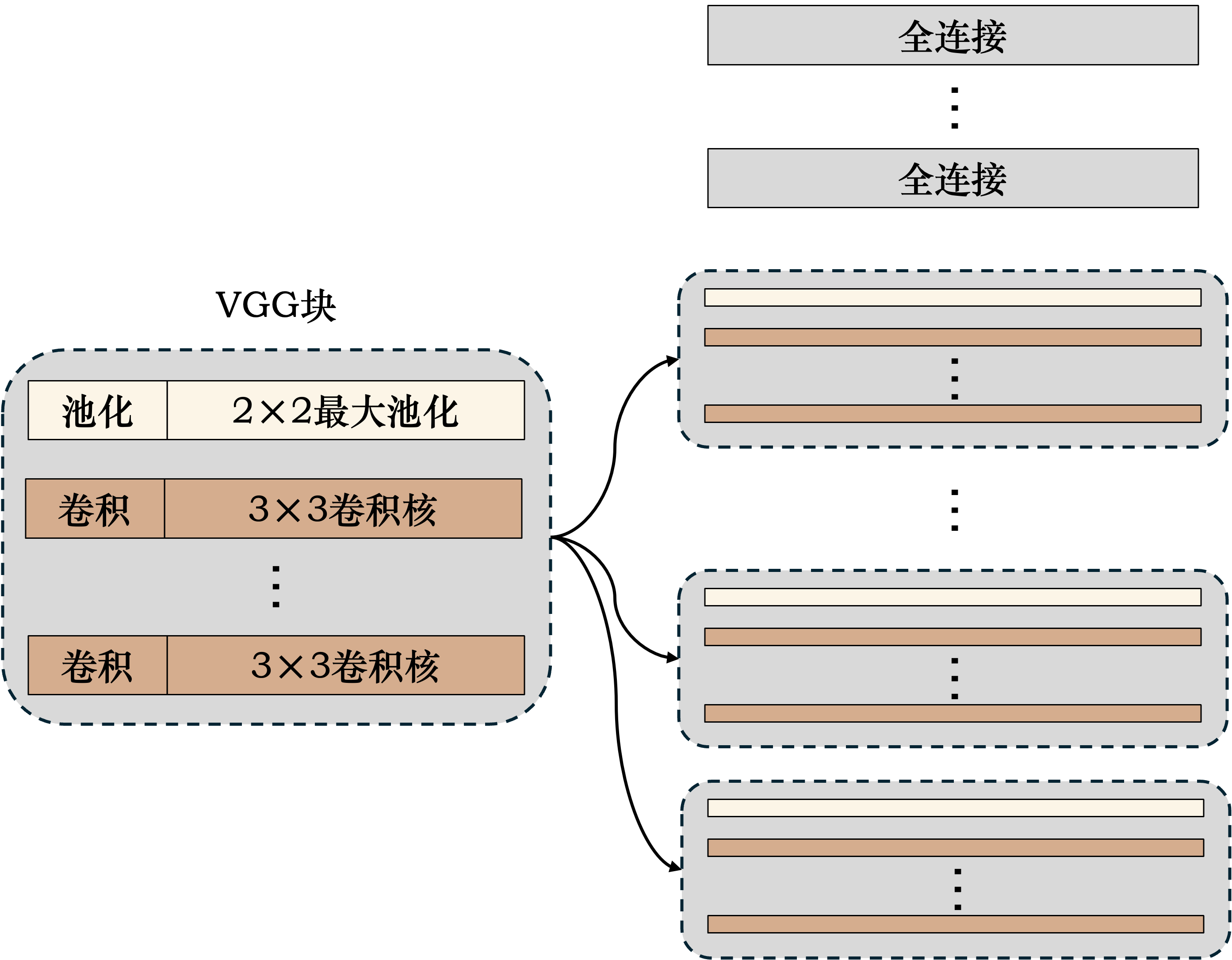
VGG_block

图 16 VGG块与VGG网络的结构#

\(\hspace{1.5em}\) 通过这样模块化的设计，VGG网络可以通过简单的堆叠VGG块来构建更深的网络，为深度卷积神经网络的发展提供了重要的参考。

MobileNet#

\(\hspace{1.5em}\) MobileNet是由Google提出的一种轻量级卷积神经网络架构，专为移动和嵌入式设备上的计算而设计。它通过减少模型的计算量和参数数量，实现了在资源受限的设备上运行深度学习模型的可能性。MobileNet是以高效性和低功耗为主要目标，特别适合实时图像处理和计算能力有限的设备。其核心思想是使用深度可分离卷积（Depthwise Separable Convolution）来替代传统的卷积操作，从而减少计算量和参数数量。深度可分离卷积的结构如下所示：

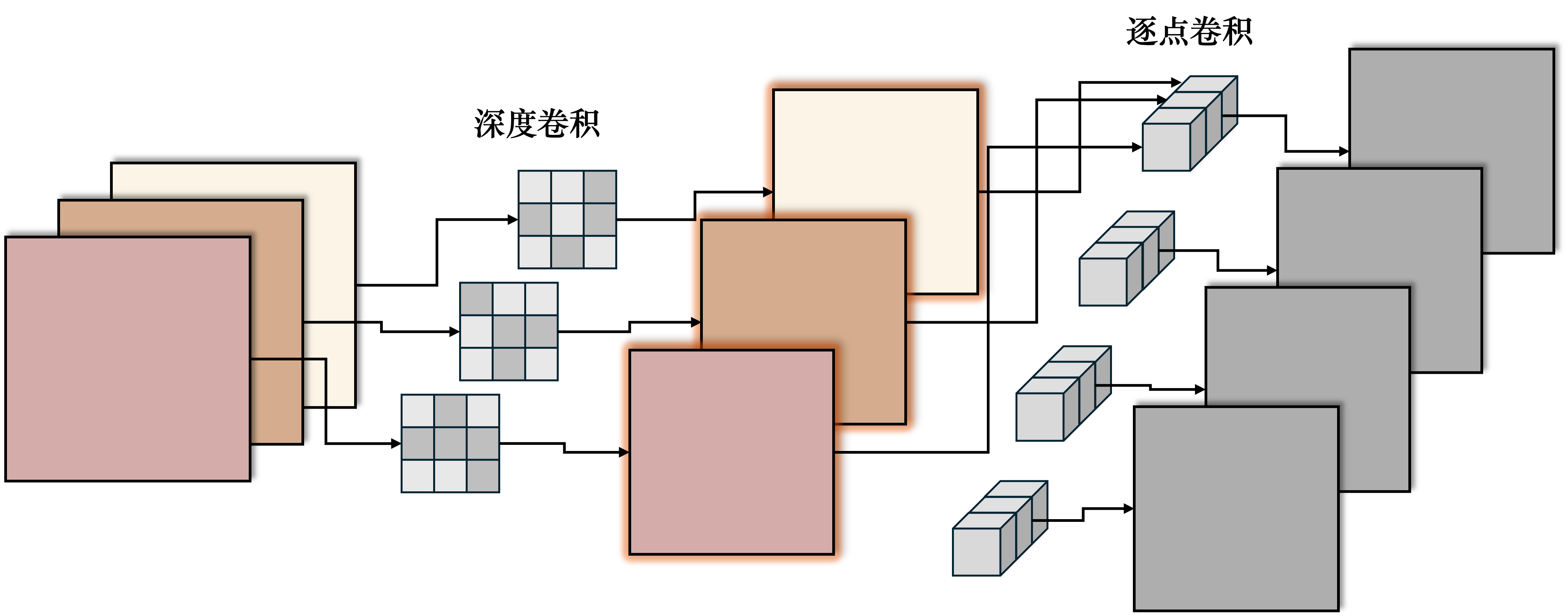
Depthwise_conv

图 17 深度可分离卷积的结构#

\(\hspace{1.5em}\) 深度可分离卷积是由两个操作组成的：

  1. 深度卷积（Depthwise Convolution）：深度卷积对每一个输入通道独立地应用一个卷积核。以一个3通道的输入为例，传统的卷积操作使用一个3x3x3的卷积核对输入整体进行卷积操作，输出的特征图为所有输入通道与一个卷积核的组合。而深度卷积则是对每一个通道使用分别的3x3的卷积核，最后得到3个特征图。

  2. 逐点卷积（Pointwise Convolution）：深度卷积仅仅是对输入的每一个通道进行卷积操作，得到了多个特征图，但是不同通道的特征图之间并没有进行组合。逐点卷积相当于一个传统的多通道1x1卷积操作，用于将深度卷积的输出特征图进行线性组合，得到最终的输出特征图。

\(\hspace{1.5em}\) 下面是通过 torch 实现的一个简单的深度可分离卷积模块：

 1import torch
 2import torch.nn as nn
 3
 4class DepthwiseSeparableConv(nn.Module):
 5        def __init__(self, in_channels, out_channels, stride=1):
 6                super(DepthwiseSeparableConv, self).__init__()
 7                # 深度卷积: groups=in_channels 实现每个通道独立卷积
 8                self.depthwise = nn.Conv2d(in_channels, in_channels, kernel_size=3, stride=stride, padding=1, groups=in_channels)
 9                # 逐点卷积: 1x1 卷积核，用于通道混合
10                self.pointwise = nn.Conv2d(in_channels, out_channels, kernel_size=1, stride=1)
11
12        def forward(self, x):
13                x = self.depthwise(x)
14                x = self.pointwise(x)
15                return x

Yolo#

\(\hspace{1.5em}\) 在之前的内容中，我们介绍了一些经典的神经网络结构，但是并未介绍这些网络结构在实际的计算机视觉任务中的应用，以及如何将这些网络结构应用到不同的任务中。在本节中，我们将介绍一个非常重要的目标检测网络——Yolo（You Only Look Once）。

\(\hspace{1.5em}\) 目标检测（Object Detection）是计算机视觉中的一项核心任务，旨在识别和定位图像或视频中的特定物体。与图像分类不同，图像分类仅仅是识别图像中存在的物体类别，而目标检测不仅要识别物体的类别，还需要在图像中精确定位每个物体的边界框（Bounding Box）。

\(\hspace{1.5em}\) 在Yolo之前，如R-CNN等目标检测算法通常都是Region Proposal + Classification的两步走策略。即首先通过一些算法（例如Selective Search、EdgeBoxes等）生成若干个候选区域，然后对每个候选区域进行分类。这种两步走的策略虽然取得了不错的效果，但是速度较慢，不适合实时应用。而Yolo的出现彻底改变了目标检测的思路，它将目标检测问题视为一个单一的回归问题，直接从图像中预测目标的边界框和类别概率，从而一次性完成目标检测任务。

\(\hspace{1.5em}\) 整个Yolo网络结构大概分为三个部分：特征提取网络、检测网络和后处理。其中特征提取网络通常使用预训练的卷积神经网络，例如VGG、ResNet等，用于提取图像的特征。检测网络是Yolo的核心部分，用于预测图像中的目标边界框和类别概率。后处理部分用于对检测结果进行筛选和修正，例如非极大值抑制（Non-Maximum Suppression）。在这里，我们略过特征提取网络，主要介绍Yolo的检测网络和后处理部分。

ResNet#

\(\hspace{1.5em}\) 深度残差网络（Residual Network，ResNet）是由何凯明等人在2015年提出的一种深度卷积神经网络架构。其核心思想是通过引入残差模块（Residual Block）来解决深度卷积神经网络训练过程中的梯度消失和梯度爆炸问题，从而实现更深的网络结构。残差连接这一设计对之后的深度学习模型设计产生了深远的影响，在众多著名的深度学习模型中都可以看到残差连接的身影。

\(\hspace{1.5em}\) ResNet的提出是为了解决神经网络的层数越深，性能反而越差的问题。直觉上来说，随着神经网络层数的增加，网络应该能够学习到更加复杂的特征，具有更强的表达能力。但是实际上，当网络层数增加到一定程度时，网络的性能反而会下降。出乎意料的是，这并非是由于过拟合导致的。在训练过程中，增加网络的深度会导致训练误差增加，这种现象被称为“退化”（Degradation）问题。

\(\hspace{1.5em}\) 一般来说，如果我们给一个浅层网络添加更多的层，那么新的网络即使在增加的层数上简单复制原始网络的特征映射，也应该不会比原始网络更差。ResNet正是基于这一观察提出的。ResNet通过引入残差模块，使得网络可以学习残差映射，即学习残差而不是原始映射。残差模块与ResNet的结构如下所示：

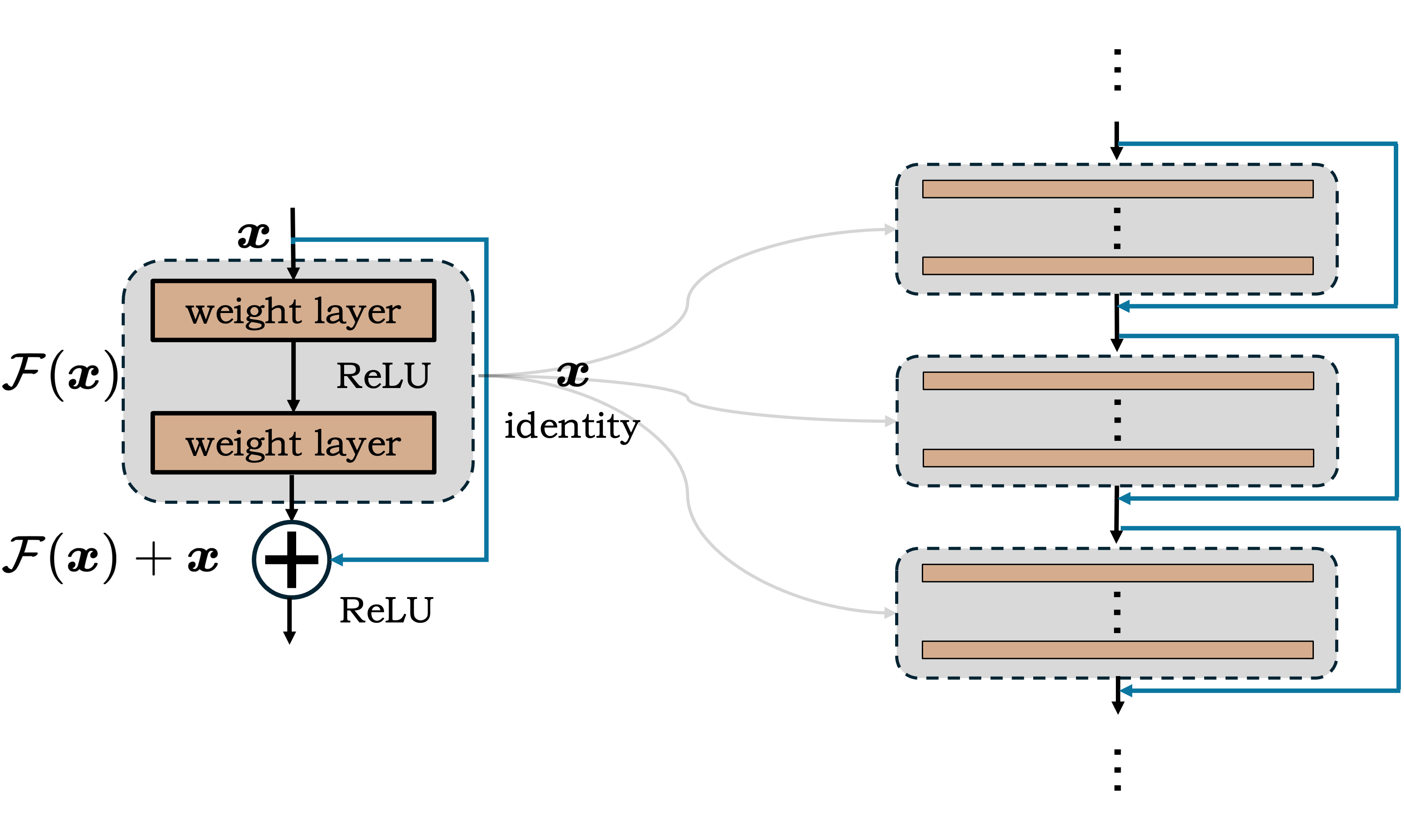
ResNet_block

图 18 ResNet的残差模块（左）与ResNet的网络结构（右）#

\(\hspace{1.5em}\) 残差模块的结构非常简单，它包含两个分支：一个是恒等映射（Identity Mapping），另一个是残差映射（Residual Mapping）。恒等映射直接将输入映射到输出，残差映射在此基础上学习一个非线性函数，最后将恒等映射和残差映射相加得到最终的输出。直观理解，如果神经网络的某一层没有作用，那么我们希望该层将输入原封不动的输出，即恒等映射。显然，对神经网络来说，学习一个为0的残差要比学习一个恒等映射要容易得多。另一方面，残差模块的引入便于信息的传递，使得较浅的网络层学习到的特征能够更为轻松的传递到较深的网络层。

\(\hspace{1.5em}\) ResNet是通过堆叠残差模块来构建深度网络的，通过引入残差连接，ResNet可以轻松地训练上百层的深度网络。我们将在下一节中动手实现一个简单的ResNet-18模型。

LeNet-5的简单实现#

\(\hspace{1.5em}\) 在这一小节中，我们将借助 torch 手动搭建卷积层与池化层，实现一个简单的卷积神经网络。我们将以 LeNet-5 为例，对 MNIST 数据集进行分类。

\(\hspace{1.5em}\) 首先让我们导入必要的库。

1# 导入相关的库
2import torch
3import torch.nn as nn
4import torch.optim as optim
5import torch.nn.functional as F
6from torch.utils.data import DataLoader
7from torchvision import datasets, transforms

这些库已经在之前的代码中有所介绍，在此不再赘述。

\(\hspace{1.5em}\) 在这里，我们简单实现一个2d卷积层。我们将利用 torch 提供的工具函数以及便捷的接口，手动实现卷积操作。下面是一个简单的卷积层的实现：

 1class MyConv2D(nn.Module):
 2    def __init__(self, in_channels, out_channels, kernel_size, stride=1, padding=0):
 3        super(MyConv2D, self).__init__()
 4        self.in_channels = in_channels
 5        self.out_channels = out_channels
 6        self.kernel_size = kernel_size
 7        self.stride = stride
 8        self.padding = padding
 9
10        # 初始化权重和偏置
11        self.weight = torch.randn(out_channels, in_channels, kernel_size, kernel_size, requires_grad=True)
12        self.bias = torch.randn(out_channels, requires_grad=True)
13
14    def forward(self, x):
15        # 手动实现卷积操作
16        batch_size, _, height, width = x.shape
17
18        # 计算输出的高度和宽度
19        out_height = (height + 2 * self.padding - self.kernel_size) // self.stride + 1
20        out_width = (width + 2 * self.padding - self.kernel_size) // self.stride + 1
21
22        # 初始化输出张量
23        out = torch.zeros((batch_size, self.out_channels, out_height, out_width))
24
25        # 对输入张量进行填充
26        if self.padding > 0:
27            x = torch.nn.functional.pad(x, (self.padding, self.padding, self.padding, self.padding))
28
29        # 手动实现卷积运算
30        for i in range(out_height):
31            for j in range(out_width):
32                region = x[:, :, i*self.stride:i*self.stride+self.kernel_size, j*self.stride:j*self.stride+self.kernel_size]
33                out[:, :, i, j] = torch.einsum('ijkl,mjkl->im', region, self.weight) + self.bias
34
35        return out

\(\hspace{1.5em}\) 在上述的代码中，我们构建了一个 MyConv2D 类，继承自 nn.Module 类。nn.Module 是 torch 中所有神经网络模块的基类，我们可以通过继承 nn.Module 类来构建自定义的神经网络模块。__init__ 是 MyConv2D 类的初始化函数，我们在这里定义了卷积层的参数，包括输入通道数、输出通道数、卷积核大小、步长和填充。此外，我们还在这个初始化函数中初始化了卷积层的权重和偏置。权重和偏置都是从标准正态分布中随机初始化的，这里我们使用 torch.randn 函数来生成随机数，并将 requires_grad 参数设置为 True，表示这些参数需要计算梯度。权重是维度为 (out_channels, in_channels, kernel_size, kernel_size) 的四维张量，偏置是维度为 (out_channels,) 的一维向量。

\(\hspace{1.5em}\) 接下来，forward 函数是 MyConv2D 类的前向传播函数。在这个函数中，我们手动实现了卷积操作。首先，我们获取输入张量的维度信息，然后计算输出张量的高度和宽度。接着，我们初始化输出张量 out，维度为 (batch_size, out_channels, out_height, out_width)。如果填充参数 padding 大于0，我们对输入张量 x 进行填充。然后，我们手动实现卷积运算。我们遍历输出张量的每一个像素，获取对应的感受野区域，然后通过 torch.einsum 函数计算卷积运算的结果。最后，我们将计算得到的结果加上偏置，得到最终的输出张量 out。

einsum：爱因斯坦求和约定

\(\hspace{1.5em}\) 爱因斯坦求和（Einstein summation convention）是物理学家阿尔伯特·爱因斯坦（对，就是那个爱因斯坦）引入的一种简洁的符号表示法，常用于描述张量运算。它的基本规则是：当在一个数学表达式中某个指标（即上标或下标）在同一个项中出现两次时，默认该项对这个指标进行求和，不再需要显式地写出求和符号。这种方法在相对论和张量分析中非常有用，因为它大大简化了复杂方程的表示。

\(\hspace{1.5em}\) 举一个简单的例子，如果我们有两个矩阵 \(\boldsymbol{A}\) 和 \(\boldsymbol{B}\)，我们可以通过爱因斯坦求和约定来表示矩阵乘法：

\[\boldsymbol{C} = A_{ij} B_{jk}\]

这里，\(i\) 和 \(k\) 是重复的指标，因此我们默认对这两个指标进行求和。因此，上述表达式等价于：

\[C_{ik} = \sum_{j} A_{ij} B_{jk}\]

\(\hspace{1.5em}\) 在 torch 中，我们可以通过 torch.einsum 函数来实现爱因斯坦求和约定。在上述代码中，我们使用 torch.einsum('ijkl,mjkl->im', region, self.weight) 来计算卷积运算的结果。这里，ijkl 和 mjkl 是张量的维度标签，->im 表示输出张量的维度标签。这个表达式等价于：

\[\text{out}_{im} = \sum_{j,k,l} \text{region}_{ijkl} \times \text{weight}_{mjkl}\]

这里，我们对 jkl 进行了求和，因此在爱因斯坦求和约定中，jkl 是重复的指标。这种表示方法大大简化了卷积运算的实现。如果想要进一步的了解 torch.einsum 函数的用法，可以参考 torch 官方文档：torch.einsum。

\(\hspace{1.5em}\) 注意到，我们在这里只写了前向传播的代码，没有写反向传播的代码。这是因为 torch 提供了自动求导的功能，我们只需要定义前向传播的计算过程，然后通过调用 backward 函数，torch 就会自动计算梯度并进行反向传播。

\(\hspace{1.5em}\) 接下来，我们手动实现一个最大池化层。

 1class NyMaxPool2D(nn.Module):
 2    def __init__(self, kernel_size, stride=None, padding=0):
 3        super(NyMaxPool2D, self).__init__()
 4        self.kernel_size = kernel_size
 5        self.stride = stride if stride is not None else kernel_size
 6        self.padding = padding
 7
 8    def forward(self, x):
 9        batch_size, channels, height, width = x.shape
10
11        # 计算输出的高度和宽度
12        out_height = (height + 2 * self.padding - self.kernel_size) // self.stride + 1
13        out_width = (width + 2 * self.padding - self.kernel_size) // self.stride + 1
14
15        # 初始化输出张量
16        out = torch.zeros((batch_size, channels, out_height, out_width))
17
18        # 对输入张量进行填充
19        if self.padding > 0:
20            x = torch.nn.functional.pad(x, (self.padding, self.padding, self.padding, self.padding))
21
22        # 手动实现最大池化操作
23        for i in range(out_height):
24            for j in range(out_width):
25                region = x[:, :, i*self.stride:i*self.stride+self.kernel_size, j*self.stride:j*self.stride+self.kernel_size]
26                out[:, :, i, j] = region.max(dim=-1)[0].max(dim=-1)[0]
27
28        return out

\(\hspace{1.5em}\) 在上述代码中，我们构建了一个 NyMaxPool2D 类，同样继承自 nn.Module 类。__init__ 是 NyMaxPool2D 类的初始化函数，我们在这里定义了池化层的参数，包括池化核大小、步长和填充。因为池化层不包含任何需要训练迭代的参数，所以在池化层的初始化中，我们并没有定义任何可训练的参数。

\(\hspace{1.5em}\) 接下来，forward 函数是 NyMaxPool2D 类的前向传播函数。在这个函数中，我们手动实现了最大池化操作。首先，我们获取输入张量的维度信息，然后计算输出张量的高度和宽度。接着，我们初始化输出张量 out，维度为 (batch_size, channels, out_height, out_width)。如果填充参数 padding 大于0，我们对输入张量 x 进行填充。然后，我们手动实现最大池化运算。我们遍历输出张量的每一个像素，获取对应的感受野区域，然后通过 max 函数计算最大池化运算的结果。最后，我们将计算得到的结果保存到输出张量 out 中。

\(\hspace{1.5em}\) 接下来，我们将使用我们手动实现的卷积层和池化层，搭建一个简单的卷积神经网络。我们以 LeNet-5 为例，搭建一个包含两个卷积层和两个池化层的卷积神经网络。

 1class MyLeNet5(nn.Module):
 2    def __init__(self):
 3        super(MyLeNet5, self).__init__()
 4        self.conv1 = MyConv2D(in_channels=1, out_channels=6, kernel_size=5, stride=1, padding=0)
 5        self.conv2 = MyConv2D(in_channels=6, out_channels=16, kernel_size=5, stride=1, padding=0)
 6        self.pool = NyMaxPool2D(kernel_size=2, stride=2)
 7        self.fc1 = nn.Linear(16*5*5, 120)
 8        self.fc2 = nn.Linear(120, 84)
 9        self.fc3 = nn.Linear(84, 10)
10
11    def forward(self, x):
12        x = self.pool(F.relu(self.conv1(x)))
13        x = self.pool(F.relu(self.conv2(x)))
14        x = x.view(-1, 16*5*5)
15        x = F.relu(self.fc1(x))
16        x = F.relu(self.fc2(x))
17        x = self.fc3(x)
18        return x

\(\hspace{1.5em}\) 在上面的代码中，我们定义了一个 MyLeNet5 类，继承自 nn.Module 类。LeNet-5的搭建方法与上一章中搭建全连接神经网络的方法类似，只是我们在这里使用我们自己实现的卷积层和池化层，使用的方法也与 torch 中内置的层一致。接下来我们定义训练函数与测试函数、导入数据集、实例化模型、定义损失函数与优化器，这些代码的构建与之前的内容基本一致，此处不再赘述。

 1# 训练函数
 2def train(model, train_loader, criterion, optimizer, num_epochs, device):
 3    model.train()
 4    loss_list = []
 5    for epoch in range(num_epochs):
 6        loss_list.append([])
 7        for batch_idx, (data, target) in enumerate(train_loader):
 8            data, target = data.to(device), target.to(device)
 9            optimizer.zero_grad()
10            output = model(data)
11            loss = criterion(output, target)
12            loss.backward()
13            optimizer.step()
14            if batch_idx % 100 == 0:
15                print(f'Epoch {epoch}, Batch {batch_idx}, Loss: {loss.item()}')
16                loss_list[-1].append(loss.item())
17    return loss_list
18
19
20
21# 测试函数
22def test(model, test_loader, criterion):
23    model.eval()
24    test_loss = 0
25    correct = 0
26    with torch.no_grad():
27        for data, target in test_loader:
28            data, target = data.to(device), target.to(device)
29            output = model(data)
30            test_loss += criterion(output, target).item()
31            pred = output.argmax(dim=1, keepdim=True)
32            correct += pred.eq(target.view_as(pred)).sum().item()
33    test_loss /= len(test_loader.dataset)
34    accuracy = 100. * correct / len(test_loader.dataset)
35    print(f'Test Loss: {test_loss:.4f}, Accuracy: {accuracy:.2f}%')
36
37
38# 加载训练集和测试集
39trainset = datasets.MNIST('~/.pytorch/MNIST_data/', download=True, train=True,
40                transform=transforms.ToTensor())
41trainloader = DataLoader(trainset, batch_size=64, shuffle=True)
42
43testset = datasets.MNIST('~/.pytorch/MNIST_data/', download=True, train=False,
44                transform=transforms.ToTensor())
45testloader = DataLoader(testset, batch_size=64, shuffle=False)
46
47# 实例化模型
48model = MyLeNet5().to(device)
49# 定义损失函数
50criterion = nn.CrossEntropyLoss()
51# 定义优化器
52optimizer = optim.Adam(model.parameters(), lr=0.001)

\(\hspace{1.5em}\) 下面我们开始训练模型：

1loss_list = train(model, trainloader, criterion, optimizer, 5, device)

\(\hspace{1.5em}\) 训练的输出如下：

Epoch 0, Batch 0, Loss: 5.012927532196045
Epoch 0, Batch 100, Loss: 0.32079795002937317
Epoch 0, Batch 200, Loss: 0.41134676337242126
Epoch 0, Batch 300, Loss: 0.11352159082889557
Epoch 0, Batch 400, Loss: 0.11403784155845642
Epoch 0, Batch 500, Loss: 0.38313722610473633
Epoch 0, Batch 600, Loss: 0.10986088216304779
Epoch 0, Batch 700, Loss: 0.32547783851623535
Epoch 0, Batch 800, Loss: 0.10511747002601624
Epoch 0, Batch 900, Loss: 0.07070255279541016
Epoch 1, Batch 0, Loss: 0.07353295385837555
Epoch 1, Batch 100, Loss: 0.15561126172542572
Epoch 1, Batch 200, Loss: 0.15481063723564148
Epoch 1, Batch 300, Loss: 0.307869553565979
Epoch 1, Batch 400, Loss: 0.20942552387714386
Epoch 1, Batch 500, Loss: 0.15707261860370636
Epoch 1, Batch 600, Loss: 0.2969551384449005
Epoch 1, Batch 700, Loss: 0.22497686743736267
Epoch 1, Batch 800, Loss: 0.0532771572470665
Epoch 1, Batch 900, Loss: 0.20364871621131897
Epoch 2, Batch 0, Loss: 0.27998217940330505
Epoch 2, Batch 100, Loss: 0.056895606219768524
...
Epoch 4, Batch 600, Loss: 0.012014992535114288
Epoch 4, Batch 700, Loss: 0.09359798580408096
Epoch 4, Batch 800, Loss: 0.2852364182472229
Epoch 4, Batch 900, Loss: 0.01731695607304573

\(\hspace{1.5em}\) 让我们画出每个epoch的训练损失：

1plt.figure(figsize=(10, 5))
2for epoch, loss in enumerate(loss_list):
3    plt.plot(loss, lw=2, marker='o', label=f'Epoch {epoch}')
4plt.xlabel('Batch', fontsize=14)
5plt.ylabel('Training Loss', fontsize=14)
6plt.legend(fontsize=14)
7plt.show()

\(\hspace{1.5em}\) 输出如下：

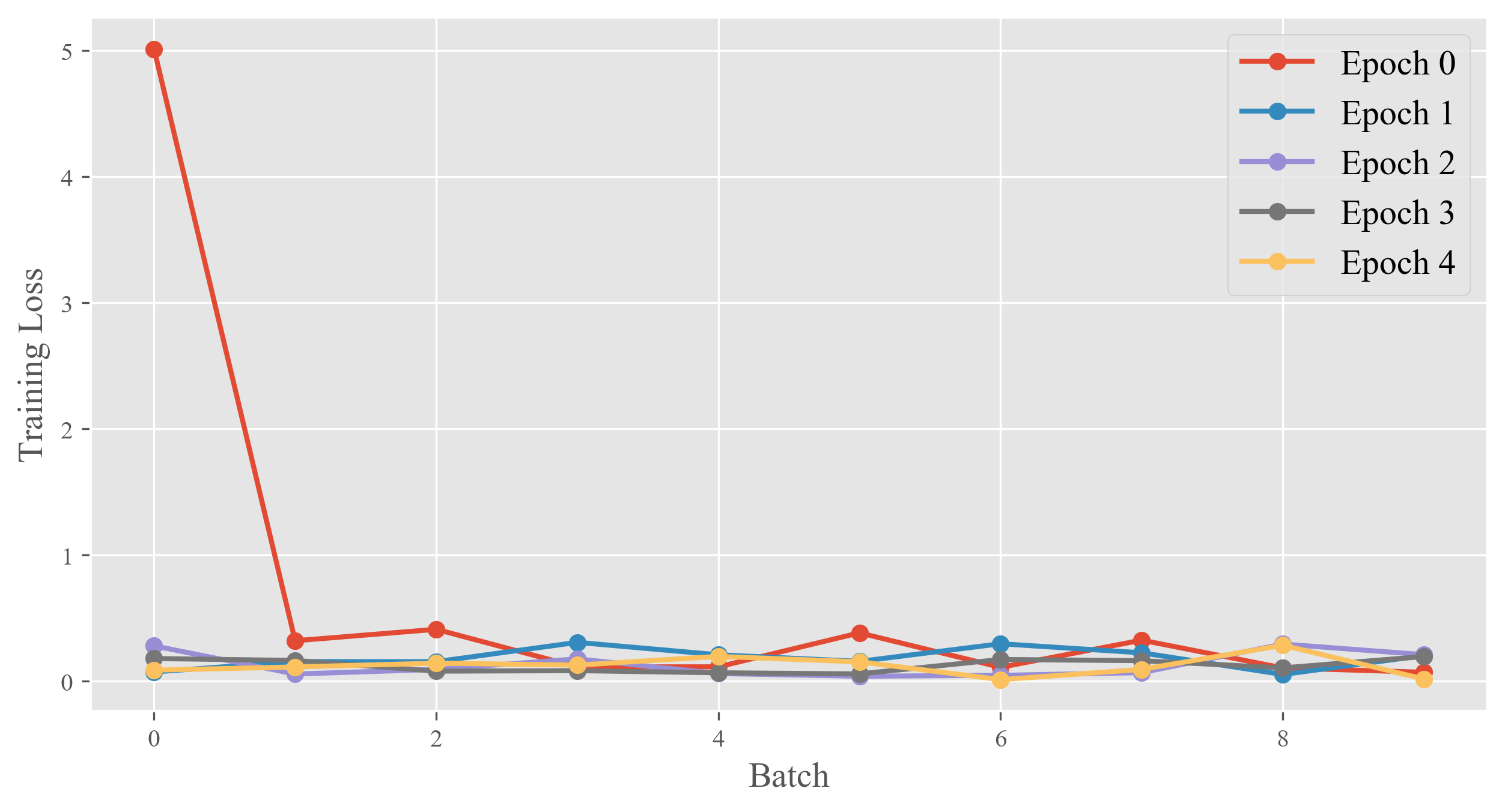
LeNet5_loss 训练损失

\(\hspace{1.5em}\) 可以看到，其实在第一个epoch中，模型已经很好的收敛了。接下来我们在测试集上测试模型的分类正确率：

1test(model, testloader, criterion)

\(\hspace{1.5em}\) 输出如下：

Test Loss: 0.0013, Accuracy: 97.28%

\(\hspace{1.5em}\) 可以看到，即便是结构简单的 LeNet-5 ，以及没有细致调试过的参数，也能在 MNIST 数据集上取得超过97%的准确率。这充分说明卷积神经网络在图像分类任务上的优越性。需要注意的是，我们自己实现的卷积层和池化层的效率并不高，因此在实际应用中，我们更多地会使用 torch 提供的内置卷积层和池化层，这些层的实现更加高效，同时也支持GPU加速。在下一小节中，我们将使用 torch 提供的内置卷积层和池化层，搭建一个更加复杂的 AlexNet ，对 CIFAR-10 数据集进行分类。

用AlexNet对CIFAR-10数据集进行分类#

\(\hspace{1.5em}\) 现在，我们将使用 AlexNet 对 CIFAR-10 数据集进行分类。 CIFAR-10 （Canadian Institute for Advanced Research, 10 classes）是一个广泛使用的小型图像分类数据集，由加拿大多伦多大学的 Alex Krizhevsky、Vinod Nair 和 Geoffrey Hinton 开发。该数据集包含60,000张32x32像素的彩色图像，分为10个类别，每个类别有6,000张图像。CIFAR-10 数据集的图像涵盖了现实生活中的10种常见物体类别：飞机、汽车、鸟类、猫、鹿、狗、青蛙、马、船和卡车。 CIFAR-10 数据集通常用于计算机视觉领域的图像分类任务，因为其图像尺寸较小且类别数量适中，非常适合作为模型训练和评估的标准基准。数据集被分为50,000张训练图像和10,000张测试图像，用于评估模型的泛化性能。

\(\hspace{1.5em}\) 在本小节中，由于 AlexNet 的模型规模比之前的 LeNet 模型更大， CIFAR-10 数据集中图像的维度为 3x32x32 ，也大于之前所使用的 MNIST 数据集，因此我们将首次尝试使用GPU来加速训练过程。

图形处理单元（Graphics Processing Unit, GPU）

图形处理器（Graphics Processing Unit, GPU）是一种专门用于图形处理的处理器，由于其高并行性和强大的计算能力，GPU 也被广泛应用于深度学习领域。在深度学习中，GPU 可以加速神经网络的训练和推理过程，提高计算效率。PyTorch 支持使用 GPU 进行计算，可以通过 torch.cuda 模块来实现。 CUDA 是 NVIDIA 公司推出的并行计算平台和编程模型，它允许开发者使用 C/C++、 Python 等语言直接调用 GPU 的计算能力。PyTorch 通过 torch.cuda 模块封装了 CUDA 的接口，提供了一系列的函数和类，方便用户在 PyTorch 中使用 GPU 进行计算。

\(\hspace{1.5em}\) 一如既往，我们首先导入本节实验所需的库，并设置随机种子。

 1import numpy as np
 2import matplotlib.pyplot as plt
 3import torch
 4import torch.nn as nn
 5import torch.optim as optim
 6import torch.nn.functional as F
 7from torch.utils.data import DataLoader
 8from torchvision import datasets, transforms
 9
10# 设置随机数种子
11np.random.seed(42)
12torch.manual_seed(42)
13torch.cuda.manual_seed_all(42) # 这次我们用了GPU，因此需要设置cuda的随机种子
14
15# 设置GPU
16device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

在上面的代码中，与之前不同的是，我们首次使用了 torch.cuda 模块，通过 torch.cuda.is_available() 函数判断当前环境是否支持 CUDA。在这里，我们使用 torch.device 类来指定模型运行的设备，如果当前环境支持 CUDA ，则使用 GPU 进行计算，否则使用 CPU 进行计算。

\(\hspace{1.5em}\) 接下来，我们搭建 AlexNet 模型。 在上一小节中，我们实现了卷积层、池化层，但是在这里，我们将使用 torch.nn 模块中的 Conv2d 和 MaxPool2d 类来构建卷积层和池化层。 参考之前的模型结构，我们通过下面的代码搭建 AlexNet 模型。

 1class AlexNet(nn.Module):
 2    def __init__(self, num_classes=10):
 3        super(AlexNet, self).__init__()
 4        self.features = nn.Sequential(
 5            nn.Conv2d(3, 96, kernel_size=11, stride=4),
 6            nn.ReLU(inplace=True),
 7            nn.LocalResponseNorm(size=5, alpha=0.0001, beta=0.75, k=2),  # LRN层
 8            nn.MaxPool2d(kernel_size=3, stride=2),
 9            nn.Conv2d(96, 256, kernel_size=5, padding=2),
10            nn.ReLU(inplace=True),
11            nn.LocalResponseNorm(size=5, alpha=0.0001, beta=0.75, k=2),  # LRN层
12            nn.MaxPool2d(kernel_size=3, stride=2),
13            nn.Conv2d(256, 384, kernel_size=3, padding=1),
14            nn.ReLU(inplace=True),
15            nn.Conv2d(384, 384, kernel_size=3, padding=1),
16            nn.ReLU(inplace=True),
17            nn.Conv2d(384, 256, kernel_size=3, padding=1),
18            nn.ReLU(inplace=True),
19            nn.MaxPool2d(kernel_size=3, stride=2),
20        )
21        self.avgpool = nn.AdaptiveAvgPool2d((6, 6))
22        self.classifier = nn.Sequential(
23            nn.Dropout(),
24            nn.Linear(256 * 6 * 6, 4096),
25            nn.ReLU(inplace=True),
26            nn.Dropout(),
27            nn.Linear(4096, 4096),
28            nn.ReLU(inplace=True),
29            nn.Linear(4096, num_classes),
30        )
31
32    def forward(self, x):
33        x = self.features(x)
34        x = self.avgpool(x)
35        x = torch.flatten(x, 1)
36        x = self.classifier(x)
37        return x

\(\hspace{1.5em}\) 在上面的代码中，我们使用了 torch.nn 模块中的 Conv2d 类来构建卷积层， MaxPool2d 类来构建池化层。 在 AlexNet 中，还有一个特殊的层，即局部响应归一化（Local Response Normalization, LRN）层，它是一种归一化方法，用于抑制神经元的活跃度，防止过拟合。但是在后续的研究中发现，LRN 层的效果并不明显，因此在一些新的模型中已经不再使用 LRN 层。在这里，我们仅作为 AlexNet 的实现，调用 torch.nn 模块中的 LocalResponseNorm 类来构建 LRN 层。在之后的实验中，我们将不再使用 LRN 层。

\(\hspace{1.5em}\) 我们在之前章节的训练函数和测试函数上稍作修改，以适应GPU的计算。

# 训练模型
def train(model, train_loader, criterion, optimizer, num_epochs, device):
    model.train()
    loss_list = []
    for epoch in range(num_epochs):
        loss_list.append([])
        for batch_idx, (data, target) in enumerate(train_loader):
            data, target = data.to(device), target.to(device)
            optimizer.zero_grad()
            output = model(data)
            loss = criterion(output, target)
            loss.backward()
            optimizer.step()
            if batch_idx % 100 == 0:
                print(f'Epoch {epoch}, Batch {batch_idx}, Loss: {loss.item()}')
                loss_list[-1].append(loss.item())
    return loss_list


# 测试模型
def test(model, test_loader, criterion):
    model.eval()
    test_loss = 0
    correct = 0
    with torch.no_grad():
        for data, target in test_loader:
            data, target = data.to(device), target.to(device)
            output = model(data)
            test_loss += criterion(output, target).item()
            pred = output.argmax(dim=1, keepdim=True)
            correct += pred.eq(target.view_as(pred)).sum().item()
    test_loss /= len(test_loader.dataset)
    accuracy = 100. * correct / len(test_loader.dataset)
    print(f'Test Loss: {test_loss:.4f}, Accuracy: {accuracy:.2f}%')

\(\hspace{1.5em}\) 之所以需要修改训练函数和测试函数，是因为我们需要将数据和模型移动到GPU上进行计算。在GPU上进行计算时，需要将数据和模型的参数都移动到GPU上，这样才能充分利用GPU的计算能力。在训练和测试函数中，我们使用 data.to(device) 和 target.to(device) 将数据移动到GPU上，在后面的代码中，我们还需要使用 model.to(device) 将模型移动到GPU上。接下来，我们导入CIFAR-10数据集，并对数据进行预处理。

 1transform = transforms.Compose([
 2transforms.Resize((227, 227)),
 3transforms.ToTensor(),
 4transforms.Normalize((0.485, 0.456, 0.406), (0.229, 0.224, 0.225))
 5])
 6train_dataset = datasets.CIFAR10(root='./data', train=True, download=True, transform=transform)
 7trainloader = DataLoader(train_dataset, batch_size=128, shuffle=True, num_workers=10)
 8
 9test_dataset = datasets.CIFAR10(root='./data', train=False, download=True, transform=transform)
10testloader = DataLoader(test_dataset, batch_size=128, shuffle=False, num_workers=10)

\(\hspace{1.5em}\) 上面的代码中，我们首先定义了一个 transform ，它是一个 Compose 对象，包含了三个操作： Resize 、 ToTensor 和 Normalize 。其中：

    4AlexNet的输入尺寸为 227x227 ，而 CIFAR-10 数据集的图像尺寸为 32x32 ，因此我们需要将 CIFAR-10 数据集的图像尺寸调整为 227x227 。实际应用中并不推荐这样做，因为这样会消耗更多的计算资源，并且可能会导致模型过拟合。

  1. Resize 用于将图像的大小调整为 227x227 4AlexNet的输入尺寸为 227x227 ，而 CIFAR-10 数据集的图像尺寸为 32x32 ，因此我们需要将 CIFAR-10 数据集的图像尺寸调整为 227x227 。实际应用中并不推荐这样做，因为这样会消耗更多的计算资源，并且可能会导致模型过拟合。，这是AlexNet的输入尺寸；

  2. ToTensor 用于将PIL图像或者 numpy.ndarray 转换为 torch.Tensor ；

  3. Normalize 用于对图像进行标准化。在参数中，第一个元组表示均值，第二个元组表示标准差。这里我们使用ImageNet数据集的均值和标准差进行标准化，这是一个常用的标准化方法。

\(\hspace{1.5em}\) 接着，我们使用 datasets.CIFAR10 类加载 CIFAR-10 数据集，其中 root 参数指定了数据集的存储路径， train 参数指定了是否加载训练集， transform 参数指定了对图像进行的预处理操作， download 参数指定了是否下载数据集。然后，我们使用 DataLoader 类创建了训练集和测试集的数据加载器 trainloader 和 testloader ，其中 batch_size 参数指定了每个批次的样本数量， shuffle 参数指定了是否打乱数据集，对于训练集我们打乱数据集，对于测试集我们不打乱数据集。

\(\hspace{1.5em}\) 下面我们实例化一个 AlexNet 模型，并进行训练。原始论文中， AlexNet 使用了 SGD 优化器，但是在这里，我们使用 Adam 优化器, 并设置学习率为 5e-4 ，这里的 5e-4 表示 \(5 \times 10^{-4}\) 。

1# 实例化模型
2model = AlexNet().to(device)
3# 定义损失函数
4criterion = nn.CrossEntropyLoss()
5# 定义优化器
6optimizer = optim.Adam(model.parameters(), lr=5e-4)
7# 训练模型
8loss_list = train(model, trainloader, criterion, optimizer, 25, device)

\(\hspace{1.5em}\) 注意在上面的代码中，我们设置了 device 变量，用于指定模型运行的设备，如果当前环境支持 CUDA ，则使用 GPU 进行计算，否则使用 CPU 进行计算。

训练输出如下：

Epoch 0, Batch 0, Loss: 2.3031015396118164
Epoch 0, Batch 100, Loss: 1.8027007579803467
Epoch 0, Batch 200, Loss: 1.5465164184570312
Epoch 0, Batch 300, Loss: 1.406746745109558
Epoch 1, Batch 0, Loss: 1.16340172290802
Epoch 1, Batch 100, Loss: 1.1709628105163574
Epoch 1, Batch 200, Loss: 0.8591127395629883
Epoch 1, Batch 300, Loss: 0.9119205474853516
Epoch 2, Batch 0, Loss: 0.9254726767539978
Epoch 2, Batch 100, Loss: 1.0733277797698975
Epoch 2, Batch 200, Loss: 0.9020097255706787
Epoch 2, Batch 300, Loss: 0.9042439460754395
Epoch 3, Batch 0, Loss: 0.8871455192565918
Epoch 3, Batch 100, Loss: 0.7843882441520691
Epoch 3, Batch 200, Loss: 0.8064925670623779
Epoch 3, Batch 300, Loss: 0.7478532195091248
Epoch 4, Batch 0, Loss: 0.705902636051178
...
Epoch 24, Batch 200, Loss: 0.2242554873228073
Epoch 24, Batch 300, Loss: 0.22900965809822083

可以看到，随着训练的进行，损失逐渐减小，模型逐渐收敛。我们在测试集上进行测试

1test(model, testloader, criterion)

测试输出如下：

Test Loss: 0.0061, Accuracy: 80.11%

从测试结果来看，尽管我们没有细致调整超参数、使用数据增强等技巧，但是 AlexNet 在 CIFAR-10 数据集上仍然取得了不错的效果，测试准确率达到了 80.11% 。

用Resnet对CIFAR-10数据集进行分类#

在本节中，我们将使用ResNet-18模型对CIFAR-10数据集进行分类。ResNet-18是指包含18个卷积层的ResNet模型，是ResNet系列中的一个较小的模型。我们将在本章中采用数据增强的方法，并应用Batch Normalization技术，以提高模型的性能。

\(\hspace{1.5em}\) 首先，我们需要导入一些必要的库，并设置随机数种子。

 1import numpy as np
 2import matplotlib.pyplot as plt
 3import torch
 4import torch.nn as nn
 5import torch.optim as optim
 6import torch.nn.functional as F
 7from torch.utils.data import DataLoader
 8from torchvision import datasets, transforms
 9
10# 设置随机数种子
11np.random.seed(42)
12torch.manual_seed(42)
13torch.cuda.manual_seed_all(42) # 这次我们用了GPU，因此需要设置cuda的随机种子

\(\hspace{1.5em}\) 接下来我们定义一个Resnet的基本模块，即残差块。在ResNet中，每个残差块由两个卷积层组成，每个卷积层后面跟着一个Batch Normalization层。在这里，我们定义了一个基本的残差块，如下所示：

 1class BasicBlock(nn.Module):
 2    # 定义扩展因子，用于调整输出通道数
 3    expansion = 1
 4
 5    def __init__(self, in_channels, out_channels, stride=1):
 6        """
 7        初始化 BasicBlock 模块。
 8
 9        参数:
10        - in_channels: 输入特征图的通道数
11        - out_channels: 输出特征图的通道数
12        - stride: 卷积步长，默认为 1
13        """
14        super(BasicBlock, self).__init__()
15
16        # 第一个卷积层：3x3 卷积，用于提取特征
17        self.conv1 = nn.Conv2d(in_channels, out_channels, kernel_size=3, stride=stride, padding=1, bias=False)
18        # 第一个批归一化层：对卷积后的输出进行归一化
19        self.bn1 = nn.BatchNorm2d(out_channels)
20
21        # 第二个卷积层：3x3 卷积，用于进一步提取特征
22        self.conv2 = nn.Conv2d(out_channels, out_channels, kernel_size=3, stride=1, padding=1, bias=False)
23        # 第二个批归一化层：对卷积后的输出进行归一化
24        self.bn2 = nn.BatchNorm2d(out_channels)
25
26        # 定义 shortcut 连接（残差连接）
27        self.shortcut = nn.Sequential()  # 默认 shortcut 是恒等映射（identity mapping）
28
29        # 如果步长不为 1 或输入通道数与输出通道数不匹配，则需要调整 shortcut
30        if stride != 1 or in_channels != self.expansion * out_channels:
31            self.shortcut = nn.Sequential(
32                # 1x1 卷积，用于调整通道数和空间尺寸
33                nn.Conv2d(in_channels, self.expansion * out_channels, kernel_size=1, stride=stride, bias=False),
34                # 批归一化层
35                nn.BatchNorm2d(self.expansion * out_channels)
36            )
37
38    def forward(self, x)
39        # 第一层卷积 + 批归一化 + ReLU 激活
40        out = F.relu(self.bn1(self.conv1(x)))
41
42        # 第二层卷积 + 批归一化
43        out = self.bn2(self.conv2(out))
44
45        # 将 shortcut 的输出与主路径的输出相加（残差连接）
46        out += self.shortcut(x)
47
48        # 对相加后的结果应用 ReLU 激活
49        out = F.relu(out)
50
51        return out

\(\hspace{1.5em}\) 在上面的代码中，我们首先在类中定义了一个扩展因子 expansion ，用于调整输出通道数。具体来说， expansion 为 1 时，输出通道数与输入通道数相同； expansion 大于 1 时，输出通道数为 expansion 倍的输入通道数。在 ResNet-18 模型中， expansion 的值为 1。如果我们使用 ResNet-50 模型， expansion 的值将为 4。

\(\hspace{1.5em}\) 在一个残差块中，我们首先定义了两个卷积层，每个卷积层后面跟着一个 Batch Normalization 层。残差链接是通过 shortcut 实现的，我们通过定义一个空的 nn.Sequential() 对象来表示恒等映射（identity mapping）。如果步长不为 1 或输入通道数与输出通道数不匹配，则需要调整 shortcut ，通过一个 1x1 卷积层来调整通道数和空间尺寸。在 forward 函数中，我们首先对输入应用第一个卷积层、 Batch Normalization 层和 ReLU 激活函数，然后对输出应用第二个卷积层和 Batch Normalization 层。最后，我们将 shortcut 的输出与主路径的输出相加，并对相加后的结果应用 ReLU 激活函数。

\(\hspace{1.5em}\) 接下来，我们定义 ResNet 模型。

 1class ResNet(nn.Module):
 2    def __init__(self, block, num_blocks, num_classes=10):
 3        """
 4        初始化 ResNet 模型。
 5
 6        参数:
 7        - block: 残差块类型（如 BasicBlock）
 8        - num_blocks: 每个阶段的残差块数量（如 [2, 2, 2, 2] 对应 ResNet-18）
 9        - num_classes: 分类任务的类别数
10        """
11        super(ResNet, self).__init__()
12
13        # 初始通道数
14        self.in_channels = 64
15
16        # 初始卷积层：3x3 卷积，用于提取初步特征
17        self.conv1 = nn.Conv2d(3, 64, kernel_size=3, stride=1, padding=1, bias=False)
18        # 批归一化层：对卷积后的输出进行归一化
19        self.bn1 = nn.BatchNorm2d(64)
20
21        # 构建 4 个阶段的残差块堆叠
22        self.layer1 = self._make_layer(block, 64, num_blocks[0], stride=1)  # 第一阶段
23        self.layer2 = self._make_layer(block, 128, num_blocks[1], stride=2)  # 第二阶段
24        self.layer3 = self._make_layer(block, 256, num_blocks[2], stride=2)  # 第三阶段
25        self.layer4 = self._make_layer(block, 512, num_blocks[3], stride=2)  # 第四阶段
26
27        # 全连接层：将特征向量映射到类别数量
28        self.linear = nn.Linear(512 * block.expansion, num_classes)
29
30    def _make_layer(self, block, out_channels, num_blocks, stride):
31        """
32        构建一个阶段的残差块堆叠。
33
34        参数:
35        - block: 残差块类型（如 BasicBlock）
36        - out_channels: 输出通道数
37        - num_blocks: 残差块数量
38        - stride: 第一个残差块的步长
39
40        返回:
41        - nn.Sequential: 一个阶段的残差块堆叠
42        """
43        # 定义每个残差块的步长列表
44        # 第一个残差块使用指定的 stride，后续残差块使用 stride=1
45        strides = [stride] + [1] * (num_blocks - 1)
46        layers = []
47
48        # 构建每个残差块
49        for stride in strides:
50            # 添加一个残差块
51            layers.append(block(self.in_channels, out_channels, stride))
52            # 更新输入通道数
53            self.in_channels = out_channels * block.expansion
54
55        # 将残差块堆叠成一个序列
56        return nn.Sequential(*layers)
57
58    def forward(self, x):
59        """
60        前向传播函数。
61
62        参数:
63        - x: 输入图像
64
65        返回:
66        - out: 分类结果
67        """
68        # 初始卷积层 + 批归一化 + ReLU 激活
69        out = F.relu(self.bn1(self.conv1(x)))
70
71        # 通过 4 个阶段的残差块堆叠
72        out = self.layer1(out)  # 第一阶段
73        out = self.layer2(out)  # 第二阶段
74        out = self.layer3(out)  # 第三阶段
75        out = self.layer4(out)  # 第四阶段
76
77        # 全局平均池化：将特征图的空间维度压缩为 1x1
78        out = F.avg_pool2d(out, 4)
79
80        # 展平为向量
81        out = out.view(out.size(0), -1)
82
83        # 全连接层：将特征向量映射到类别数量
84        out = self.linear(out)
85
86        return out

最后，我们定义一个 ResNet-18 模型

1def ResNet18():
2    return ResNet(BasicBlock, [2, 2, 2, 2])

接下来，我们定义训练和测试函数，这里的训练和测试函数完全参考了前面章节的代码。

 1# 训练函数
 2def train(model, train_loader, criterion, optimizer, num_epochs, device):
 3    model.train()
 4    loss_list = []
 5    for epoch in range(num_epochs):
 6        loss_list.append([])
 7        for batch_idx, (data, target) in enumerate(train_loader):
 8            data, target = data.to(device), target.to(device)
 9            optimizer.zero_grad()
10            output = model(data)
11            loss = criterion(output, target)
12            loss.backward()
13            optimizer.step()
14            if batch_idx % 100 == 0:
15                print(f'Epoch {epoch}, Batch {batch_idx}, Loss: {loss.item()}')
16                loss_list[-1].append(loss.item())
17    return loss_list
18
19# 测试函数
20def test(model, test_loader, criterion):
21    model.eval()
22    test_loss = 0
23    correct = 0
24    with torch.no_grad():
25        for data, target in test_loader:
26            data, target = data.to(device), target.to(device)
27            output = model(data)
28            test_loss += criterion(output, target).item()
29            pred = output.argmax(dim=1, keepdim=True)
30            correct += pred.eq(target.view_as(pred)).sum().item()
31    test_loss /= len(test_loader.dataset)
32    accuracy = 100. * correct / len(test_loader.dataset)
33    print(f'Test Loss: {test_loss:.4f}, Accuracy: {accuracy:.2f}%')

下面对数据集进行预处理。

 1# 数据预处理
 2transform_train = transforms.Compose([
 3    transforms.RandomCrop(32, padding=4),
 4    transforms.RandomHorizontalFlip(),
 5    transforms.ToTensor(),
 6    transforms.Normalize((0.4914, 0.4822, 0.4465), (0.2023, 0.1994, 0.2010)),
 7])
 8
 9transform_test = transforms.Compose([
10    transforms.ToTensor(),
11    transforms.Normalize((0.4914, 0.4822, 0.4465), (0.2023, 0.1994, 0.2010)),
12])
13
14# 加载CIFAR-10数据集
15train_dataset = datasets.CIFAR10(root='./data', train=True, download=True, transform=transform_train)
16test_dataset = datasets.CIFAR10(root='./data', train=False, download=True, transform=transform_test)
17
18train_loader = DataLoader(train_dataset, batch_size=128, shuffle=True, num_workers=16)
19test_loader = DataLoader(test_dataset, batch_size=128, shuffle=False, num_workers=16)

上面的代码中，我们在训练数据集上应用了两种数据增强方法：

  1. RandomCrop ：随机裁剪，将图像随机裁剪为指定大小。

  2. RandomHorizontalFlip ：随机水平翻转，将图像以0.5的概率水平翻转。

最后，我们实例化一个 ResNet-18 模型、定义损失函数和优化器。

1# 实例化 ResNet-18 模型
2device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
3model = ResNet18().to(device)
4
5# 定义损失函数和优化器
6criterion = nn.CrossEntropyLoss()
7optimizer = optim.Adam(model.parameters(), lr=0.001)
8# 学习率调度器
9scheduler = torch.optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max=200)

在这里，我们增加了一个学习率调度器 scheduler ，用于调整学习率。学习率调度器 CosineAnnealingLR 会在每个周期内调整学习率，使其在一个周期内从初始学习率下降到最小学习率，然后再上升到初始学习率。这样的学习率调度有助于模型更好地收敛。该调度器所使用的公式如下：

\[\begin{equation} \eta_t = \eta_{\text{min}} + \frac{1}{2} (\eta_{\text{max}} - \eta_{\text{min}}) (1 + \cos(\frac{T_{\text{cur}}}{T_{\text{max}}}\pi)). \end{equation}\]

其中 \(\eta_t\) 是第 \(t\) 个周期的学习率， \(\eta_{\text{min}}\) 是最小学习率， \(\eta_{\text{max}}\) 是初始学习率， \(T_{\text{cur}}\) 是当前周期， \(T_{\text{max}}\) 是总周期数。

最后，我们开始训练模型。

1# 训练模型
2loss_list = train(model, trainloader, criterion, optimizer, 100, device)

训练输出如下：

Epoch 0, Batch 0, Loss: 2.3767738342285156
Epoch 0, Batch 100, Loss: 1.5866512060165405
Epoch 0, Batch 200, Loss: 1.4910191297531128
Epoch 0, Batch 300, Loss: 1.209372878074646
Epoch 1, Batch 0, Loss: 1.1253697872161865
Epoch 1, Batch 100, Loss: 1.1158658266067505
Epoch 1, Batch 200, Loss: 0.740522027015686
Epoch 1, Batch 300, Loss: 1.1217533349990845
Epoch 2, Batch 0, Loss: 0.8137905597686768
Epoch 2, Batch 100, Loss: 0.6262770891189575
Epoch 2, Batch 200, Loss: 0.8794751167297363
...
Epoch 99, Batch 0, Loss: 0.0063345907256007195
Epoch 99, Batch 100, Loss: 0.0020089359022676945
Epoch 99, Batch 200, Loss: 0.0005474633071571589
Epoch 99, Batch 300, Loss: 0.029195604845881462

可以看到，随着训练的进行，损失逐渐减小，模型逐渐收敛。我们在测试集上进行测试。

1test(model, test_loader, criterion)

测试输出如下：

Test Loss: 0.0040, Accuracy: 91.77%