\[ \begin{align}\begin{aligned}\newcommand{\ba}{\boldsymbol{a}} \newcommand{\bb}{\boldsymbol{b}} \newcommand{\be}{\boldsymbol{e}} \newcommand{\bw}{\boldsymbol{w}} \newcommand{\bx}{\boldsymbol{x}} \newcommand{\by}{\boldsymbol{y}} \newcommand{\bz}{\boldsymbol{z}} \newcommand{\bd}{\boldsymbol{d}} \newcommand{\bv}{\boldsymbol{v}} \newcommand{\bs}{\boldsymbol{s}}\\\newcommand{\btheta}{\boldsymbol{\theta}} \newcommand{\bbeta}{\boldsymbol{\beta}} \newcommand{\bgamma}{\boldsymbol{\gamma}} \newcommand{\bsigma}{\boldsymbol{\sigma}} \newcommand{\md}{\mbox{d}} \newcommand{\bmu}{\boldsymbol{\mu}} \newcommand{\bone}{\boldsymbol{1}} \newcommand{\trans}{^{\rm\scriptsize T}} \newcommand{\var}{\mathrm{var}}\\\newcommand{\bA}{\boldsymbol{A}} \newcommand{\bB}{\boldsymbol{B}} \newcommand{\bC}{\boldsymbol{C}} \newcommand{\bD}{\boldsymbol{D}} \newcommand{\bI}{\boldsymbol{I}} \newcommand{\bM}{\boldsymbol{M}} \newcommand{\bW}{\boldsymbol{W}} \newcommand{\bX}{\boldsymbol{X}} \newcommand{\bY}{\boldsymbol{Y}} \newcommand{\bZ}{\boldsymbol{Z}} \newcommand{\cotp}{\textcolor{ #30D158FF }{TP}} \newcommand{\cotn}{\textcolor{#64D2FFFF}{TN}} \newcommand{\cofp}{\textcolor{#5E5CE6FF}{FP}} \newcommand{\cofn}{\textcolor{#BF5AF2FF}{FN}}\\\newcommand{\numcotp}{\textcolor{ #30D158FF }{50}} \newcommand{\numcotn}{\textcolor{#64D2FFFF}{30}} \newcommand{\numcofp}{\textcolor{#5E5CE6FF}{10}} \newcommand{\numcofn}{\textcolor{#BF5AF2FF}{10}}\end{aligned}\end{align} \]

序列模型

\(\hspace{1.5em}\) 在之前的章节中，我们首先学习了最基础的神经网络模型——全连接神经网络（Fully Connected Neural Network）。全连接神经网络作为线性回归的扩展，通过 多层非线性变换 来学习数据中的复杂模式。然而，在处理图像数据时，全连接神经网络的表现往往不理想。原因在于图像数据具有独特的属性，例如平移不变性和局部性（归纳偏置，inductive bias），而全连接神经网络难以有效利用这些空间结构特性，导致其在图像处理任务存在一定局限性。为了解决这个问题，我们在前一章中介绍了卷积神经网络（Convolutional Neural Network, CNN）。卷积神经网络能够有效利用图像中像素之间的空间关系，因此在图像识别、目标检测等任务中取得了显著的效果。无论是在全连接神经网络还是在卷积神经网络中，我们通常假设数据来自某个未知分布，并且所有样本都是独立同分布的（i.i.d.），即样本之间不存在自相关性（autocorrelation）。然而，在实际情况中，许多数据并不满足这一假设条件。

归纳偏置

\(\hspace{1.5em}\) 在深度学习中，这类经验特征（empirical facts）被称为“归纳偏置”（inductive bias）。它可以理解为：我们通过观察数据归纳出一定规则，对模型施加约束，从而有助于“模型选择”，即从假设空间中选择更符合现实规律的模型。

\(\hspace{1.5em}\) 例如，一篇文章中的单词是按照顺序写的，具有特定的语法结构和语义。假设我们有一个句子：“人工智能与机器学习这门课真____”，我们的目标是通过这个句子中已经出现的词来预测空白处的词。根据句子的上文，我们可以猜测空白处的词可能是“有趣”，也有可能是“困难”。但是，当我们忽略了句子中词语出现的顺序，整个句子的意思就完全不一样了。例如：“狗咬人”远没有“狗咬人”那么令人惊讶 ^{1 1}本例源自 《动手学深度学习（中文版）》 第八章，强烈推荐大家阅读该书。此外，该书作者之一 李沐 在B站提供了相关的视频课程，涵盖了深度学习基础课程以及人工智能最前沿的研究。感兴趣的同学可以通过 此链接 进行学习。。这是因为词语之间存在着一定的顺序关系，这个顺序决定了我们如何去理解这个句子。因此，我们不能简单地将它们看作是独立的。再比如在时间序列数据中（time series data），时刻 \(t\) 的观测值 \(x_t\) 通常与前一时刻的观测值 \(x_{t-1}\) 有关。在给定了序列的观测值以后，如果我们想要预测 \(t+1\) 时刻的观测值，我们就需要考虑到数据中存在的时间相依关系（time dependence）。

\(\hspace{1.5em}\) 一般来说，我们把顺序特别重要的数据称为序列数据（sequential data） ^{2 2}在时间序列分析中，依照时间顺序收集到的数据被称为时间序列数据。从这个角度来说，文本和语音数据也可以认为是依照时间顺序收集到的数据。 。假设输入数据可以表示为 \(\{ x_t \}_{t = 1}^{T}, x_t \in \mathcal{R}^d\) ，我们的目标是通过收集的到观测值来解决如下问题：

1. 时间序列预测（time series forecasting）：预测 \((x_{t+1}, x_{t+2}, \dots)\) ，即根据观测数据来预测未来的观测值；

2. 分类：预测 \(y\) ，例如根据一段文本判断该文本想要表达的情绪是正向的还是负向的（sentiment analysis）；

3. 序列到序列的转换：预测一组序列 \((y_1, y_2, \dots, y_{T{\prime}})\) ，例如在机器翻译中，根据给定的中文句子生成对应的英文句子。

序列数据建模中的数学表达

\(\hspace{1.5em}\) 从上述例子中我们可以看到，序列数据建模的核心是如何利用序列数据中的时间信息或者上下文信息来预测下一个时刻的值或者整个序列的分类标签。因此，在后续内容中，我们主要考虑以输出为 \(\{y_t\}\) 的序列建模问题为例，针对其他任务，我们会在具体问题下进行讨论。

\(\hspace{1.5em}\) 从这些例子中可以看出，序列数据的关键特性是其顺序关系，也就是相邻数据之间的相关性。如果忽视了序列中的时间相依性，模型往往无法取得理想的效果。在对序列数据进行建模和预测时，全连接神经网络和卷积神经网络通常会面临以下两个问题：

1. 无法有效捕捉序列间的依赖关系：在全连接神经网络和卷积神经网络中，并没有考虑输入序列之间的自相关性。

2. 处理变长序列的能力有限：在对序列数据进行建模时，输入和输出的 序列长度通常是不固定 的，这种变化给全连接和卷积神经网络直接处理序列数据带来了巨大挑战。

\(\hspace{1.5em}\) 为了有效地建模序列数据，我们需要基于序列数据的归纳偏置设计新的网络模型。循环神经网络（Recurrent Neural Network, RNN）是一种专门用于处理序列数据的神经网络，通过引入循环结构，使得网络在每个时间步能够“记住”之前的信息，从而捕捉到序列中的时间依赖性。这一特性使RNN在处理时间序列、文本、语音等顺序性强的数据时尤为适用。

\(\hspace{1.5em}\) 在本章中，我们会首先针对时间序列数据和文本数据的建模给出一个通用框架。然后，我们将介绍RNN及其扩展模型——包括长短期记忆网络（LSTM）和门控循环单元（GRU），以解决RNN在捕捉长期依赖信息时的局限。接着，我们将讨论这循环神经网络在序列建模中存在的局限性，并介绍注意力机制（Attention Mechanism）作为改进方法，帮助模型更精准地捕捉重要信息。最后，我们将介绍Transformer模型及其衍生的大语言模型。Transformer不依赖于传统循环结构，而是通过多头自注意力机制直接计算序列中任意位置之间的依赖关系，实现了更高效和灵活的序列处理。这种机制使得Transformer能够高效地处理长距离依赖关系，并具有出色的并行处理能力，极大地推动了自然语言处理等领域的发展。

前置知识

\(\hspace{1.5em}\) 在正式介绍模型架构之前，我们需要先理解序列数据的特点和常见的建模方法。对于时间序列数据来说，最基础的模型是自回归模型（Autoregressive Model, AR） ^{3 3}没有修过时间序列这门课的同学，可以先了解一下时间序列的基本概念。建议通过中国大学MOOC上的 《时间序列分析》 课程进行学习。 ，它通过将过去的观测值作为输入来预测未来的值，适用于具有时间依赖性的数值数据。然而，对于文本和语音等非结构化数据，我们首先需要将其转化为适合建模的数值形式，然后再进一步分析和建模。在接下来的内容中，我们将首先介绍在时间序列中广泛使用的自回归模型，帮助我们理解如何捕捉数据中的时间依赖性。然后，我们将探讨文本分析中的语言模型，了解如何对非结构化的文本数据进行建模。

自回归模型

\(\hspace{1.5em}\) 自回归模型与回归模型的不同之处在于，自回归模型是用于时间序列数据的建模。在线性回归中，我们的自变量 \(x\) 本身 是独立的；而在自回归中，我们的自变量是 \(x_t\) 与历史观测值 \((x_{t-1}, x_{t-2}, \dots)\) 之间是存在自相关性的。因此，自回归模型的目标是通过历史观测值来预测未来的观测值。以最简单的AR(1)模型为例，可以表示为：

\[x_{t} = \phi x_{t-1} + \epsilon_{t},\]

其中，\(x_{t}\) 是时刻 \(t\) 的观测值，\(\phi\) 是模型参数，\(\epsilon_{t} \sim i.i.d (0, 1)\) 是噪声项。AR（1）模型假设当前时刻的观测值只与前一时刻的观测值有关。在自回归模型中，阶数定义了当前观测值与多少阶之前的观测值相关。P阶自回归模型AR（P）的定义是： \(x_{t} = \sum_{i=1}^{P} \phi_i x_{t-i} + \epsilon_{t}\)。

\(\hspace{1.5em}\) 给定历史观测值 \(x_{1}, \dots, x_{t-1}\)，如果我们想要预测未来的观测值，我们可以通过递归地使用这个公式来计算：

\[\begin{split}\hat x_{t} &= \hat \phi x_{t-1} \\ \hat x_{t+1} &= \hat \phi \hat x_{t} \\ \hat x_{t+2} &= \hat \phi \hat x_{t+1} \\ &\vdots\end{split}\]

其中 \(\hat \phi\) 是估计的模型参数。对于AR（P）模型，我们可以用下面的公式来进行预测：

\[\begin{split}\hat x_{t} &= \sum_{i=1}^{P} \hat \phi_i x_{t-i} \\ \hat x_{t+1} &= \hat \phi_1 \hat x_{t} + \sum_{i=2}^{P} \hat \phi_i x_{t+1-i} \\ \hat x_{t+2} &= \hat \phi_1 \hat x_{t+1} + \hat \phi_2 \hat x_{t} + \sum_{i=3}^{P} \hat \phi_i x_{t+2-i} \\ &\vdots\end{split}\]

时间序列多步预测（multi-step ahead forecasting）

\(\hspace{1.5em}\) 请注意，在进行预测时，因为无法知道未来的观测值，我们通常会使用模型预测的值作为下一时刻的输入。在时间序列预测中，我们称之为迭代预测（recursive forecasting），该方法也常用于语言模型中。直接预测（direct forecasting）是多步向前预测中的另一种方法，关于两种方法的比较，参见 Recursive and direct multi-step forecasting: the best of both worlds 。

\(\hspace{1.5em}\) 我们可以看到，自回归与回归模型相比，在于引入了时间维度，并且使用了历史观测值作为自变量，当前期的观测值作为因变量，这使得模型能够捕捉到序列数据中的时间依赖。在下一章中，我们会看到循环神经网络（RNN）通过将同样的思想应用到全连接神经网络中，从而实现对序列数据的建模。

⁴本节主要聚焦于基于深度学习的语言模型，而传统的文本分析方法（如词袋模型以及基于词频或字典的文本表示方法）不在讨论范围内。对此类方法感兴趣的同学可以参考 Foundations of Statistical Natural Language Processing 一书进行学习。另外，推荐阅读一篇从统计角度探讨文本分析的综述文章 Text as data (Gentzkow et al., 2019; JEL) ，供进一步学习参考。

语言模型 ^{4 4}本节主要聚焦于基于深度学习的语言模型，而传统的文本分析方法（如词袋模型以及基于词频或字典的文本表示方法）不在讨论范围内。对此类方法感兴趣的同学可以参考 Foundations of Statistical Natural Language Processing 一书进行学习。另外，推荐阅读一篇从统计角度探讨文本分析的综述文章 Text as data (Gentzkow et al., 2019; JEL) ，供进一步学习参考。

\(\hspace{1.5em}\) 文本数据作为一种非结构化数据，在自然语言处理中占据着核心地位。为了能够在计算机中对文本数据进行有效建模，首要任务是将文本数据转换为数值形式，这样模型才能理解和处理文本信息。在本节中，我们将首先介绍一些相关的术语，并利用 Huggingface 上的预训练模型为例 ^{5 5}Huggingface 是一个自然语言处理领域的开源社区，提供了大量的预训练模型和数据集，方便用户快速构建和部署自然语言处理模型。国内镜像网站为 HF_mirror ,感兴趣的同学可以根据官网指南安装使用。 以下内容默认各位同学已经按照指南完成安装。 ，更形象地对每个术语进行阐述。然后我们将探讨如何利用 词嵌入 （word embedding）技术来将文本转化为数值表示。最后，我们将引入 语言模型 （Language Model）的概念，了解语言模型是如何对文本数据进行建模的。

术语

• 语料（corpus）：语料是指用于训练和评估模型的文本数据集。语料可以是从互联网、书籍、新闻等来源中收集的大规模文本数据，也可以是特定领域的专业文本。语料的规模和质量对模型的性能有重要影响，因此在构建语言模型时，需要选择合适的语料进行训练。假设我们研究要电影文本的情感分析，那么我们可以将 IMDB电影评论数据集 作为我们的语料。在该数据集中，包含了大量的电影评论文本，以及每条评论的情感标签（正向或负向），可以用于训练情感分析模型。下面，我们给出如何通过代码访问 Huggingface 上的数据集：

合理、高效地使用网络资源

\(\hspace{1.5em}\) 在学习深度学习时，“动手实践”（make your hands dirty）是至关重要的原则。要理解深度学习的原理和应用，需要不断地动手尝试不同的模型和数据集。为此，首先要熟悉 Python 代码的 基本语法，这是实践的基础。其次，我们需要明确自己的学习目标。明确学习目标后，我们可以通过 1. 官方教程和文档（API），了解模型或数据集的基本原理和使用方法； 2. 遇到问题时，可以通过搜索引擎查找相关资料（通常来说，你并不会是第一个遇到这个问题的人）。 本节中用到的例子，均是通过查阅官方API实现，希望大家在学习的过程中，能够熟练掌握这种查阅资料的方法。

# 通过datasets库加载IMDB电影评论数据集
# 请确保已经安装了datasets库
# 遇到网络问题请考虑使用离线模式或者使用国内镜像
from datasets import load_dataset
# 下载数据集
train_dataset = load_dataset("stanfordnlp/imdb", split="train")
# 打印数据集的大小
print('Sample size of the training data is : ', len(train_dataset))
# 打印数据集的第一条数据
print('The first sample of the training data is : \n', train_dataset[0])

\(\hspace{1.5em}\) 上述代码的运行结果如下：

Sample size of the training data is :  25000
The first sample of the training data is :
{'text': 'I rented I AM CURIOUS-YELLOW from my video store because of all the controversy that surrounded it when it was first released in 1967. I also heard that at first it was seized by U.S. customs if it ever tried to enter this country, therefore being a fan of films considered "controversial" I really had to see this for myself.<br /><br />The plot is centered around a young Swedish drama student named Lena who wants to learn everything she can about life. In particular she wants to focus her attentions to making some sort of documentary on what the average Swede thought about certain political issues such as the Vietnam War and race issues in the United States. In between asking politicians and ordinary denizens of Stockholm about their opinions on politics, she has sex with her drama teacher, classmates, and married men.<br /><br />What kills me about I AM CURIOUS-YELLOW is that 40 years ago, this was considered pornographic. Really, the sex and nudity scenes are few and far between, even then it\'s not shot like some cheaply made porno. While my countrymen mind find it shocking, in reality sex and nudity are a major staple in Swedish cinema. Even Ingmar Bergman, arguably their answer to good old boy John Ford, had sex scenes in his films.<br /><br />I do commend the filmmakers for the fact that any sex shown in the film is shown for artistic purposes rather than just to shock people and make money to be shown in pornographic theaters in America. I AM CURIOUS-YELLOW is a good film for anyone wanting to study the meat and potatoes (no pun intended) of Swedish cinema. But really, this film doesn\'t have much of a plot.',
'label': 0}

• 词表（vocabulary）：我们的语料中包含了大量的词汇，经过词元化（第三步）处理后，我们得到的是一连串的字符串（string），然而模型需要的输入是数字（向量、矩阵或者是张量）。为了解决这个问题，通常我们会构建一个词表（vocabulary），将每个词映射为一个唯一的整数。词表的大小取决于语料中的词汇量，通常会包含语料中 所有出现的词元。词表的构建是文本数据预处理的重要步骤，它将文本数据转换为模型可以处理的数值形式。除了在语料中出现的词汇，词表通常还会包含一些特殊的标记，如 <UNK> （未知词元）、 <PAD> （填充词元）、 <BOS> （句子起始词元）和 <EOS> （句子结束词元）等。下面，我们打印预训练模型中的部分词表：

# 请确保已经正确安装 ``Huggingface`` 库
from transformers import BertTokenizer
# 使用预训练的BertTokenizer
# 这里可以忽略"bert-base-uncased"，后续章节会详细介绍
tokenizer = BertTokenizer.from_pretrained("bert-base-uncased")
# 给出词表中第2013到2024个id对应的词元
vocab_slice = list(tokenizer.vocab.items())[2013:2024]
for item in vocab_slice:
   print(item)
# 特殊词元
vocab_slice = list(tokenizer.vocab.items())[100:104]
for item in vocab_slice:
   print(item)

\(\hspace{1.5em}\) 在上述代码中，我们加载了一个预训练的tokenizer，并打印了词表中的部分词元。输出结果如下：

('from', 2013)
('her', 2014)
('##s', 2015)
('she', 2016)
('you', 2017)
('had', 2018)
('an', 2019)
('were', 2020)
('but', 2021)
('be', 2022)
('this', 2023)
('[UNK]', 100)
('[CLS]', 101)
('[SEP]', 102)
('[MASK]', 103)

\(\hspace{1.5em}\) 对于每个词元，我们给出了它在词表中的索引。可以看到，词表中包含了大量的词元，每个词元都被映射为一个唯一的整数。此外，我们还引入了一些特殊的词元，如 [CLS] （句子起始词元）和 [SEP] （句子划分词元），这些词元在模型训练和推理中起到重要作用。

• 词元化（tokenization）：词元化是将文本分解成基本单元（词或子词，word or sub-word）的一种过程。通过词元化，我们可以将句子拆分为一系列的“词元”（token），为后续的数值表示做好准备。词元的划分方式可以是按词、按子词，或按字符进行，具体取决于应用需求和语言特点。下面，我们使用 Huggingface 的 BertTokenizer 来对给定句子进行词元化：

词元

\(\hspace{1.5em}\) 词元（token）是文本数据的最小单位，可以是单词、子词或字符。例如，对于“This course is interesting”这句话，如果按照单词划分，那么 this、course、is、interesting 就是四个词元；如果按照字符划分，那么 T、h、i、s、c、o、u、r、s、e、i、s、i、n、t、e、r、e、s、t、i、n、g 就是22个词元；子词划分则介于单词和字符之间，例如 interesting 可以划分为 interest 和 ##ing （子词） 。中文文本与英文文本略有不同，中文文本的词元通常是单个汉字或词语。中文词语的划分可以参照python库的 jieba 分词工具。

# 举个例子
sentence = "AI and ML course is interesting and easy!"
# 对上述句子进行词元化，得到词元和词元ID
input_ids = tokenizer(sentence)['input_ids']
tokens = tokenizer.convert_ids_to_tokens(input_ids)
# 输出
print("Tokens:", tokens)
print("Token IDs:", input_ids)

\(\hspace{1.5em}\) 在上述代码中，使用之前加载好的 tokenizer 对给定的句子进行词元化。输出结果如下：

Tokens: ['[CLS]', 'ai', 'and', 'ml', 'course', 'is', 'interesting', 'and', 'easy', '!', '[SEP]']
Token IDs: [101, 9932, 1998, 19875, 2607, 2003, 5875, 1998, 3733, 999, 102]

\(\hspace{1.5em}\) 可以看到，句子被成功划分为一系列词元，每个词元都被映射为唯一的整数。此外，词元 and 出现了两次，但映射到了相同的整数值。同时，我们发现 BertTokenizer 还引入了两个特殊词元 [CLS] 和 [SEP]，这两个词元的索引与词元表中的索引相对应。这些特殊词元在模型训练和推理中起到重要作用，我们将在后续章节中详细介绍。

• 词嵌入（word embedding）：词嵌入是一种将文本中的词映射为数值向量的技术，帮助模型在高维空间中表示和处理语义关系。在词嵌入中，每个词被映射为一个向量，使得具有相似语义的词在向量空间中彼此接近。下图展示了词嵌入的示意图：

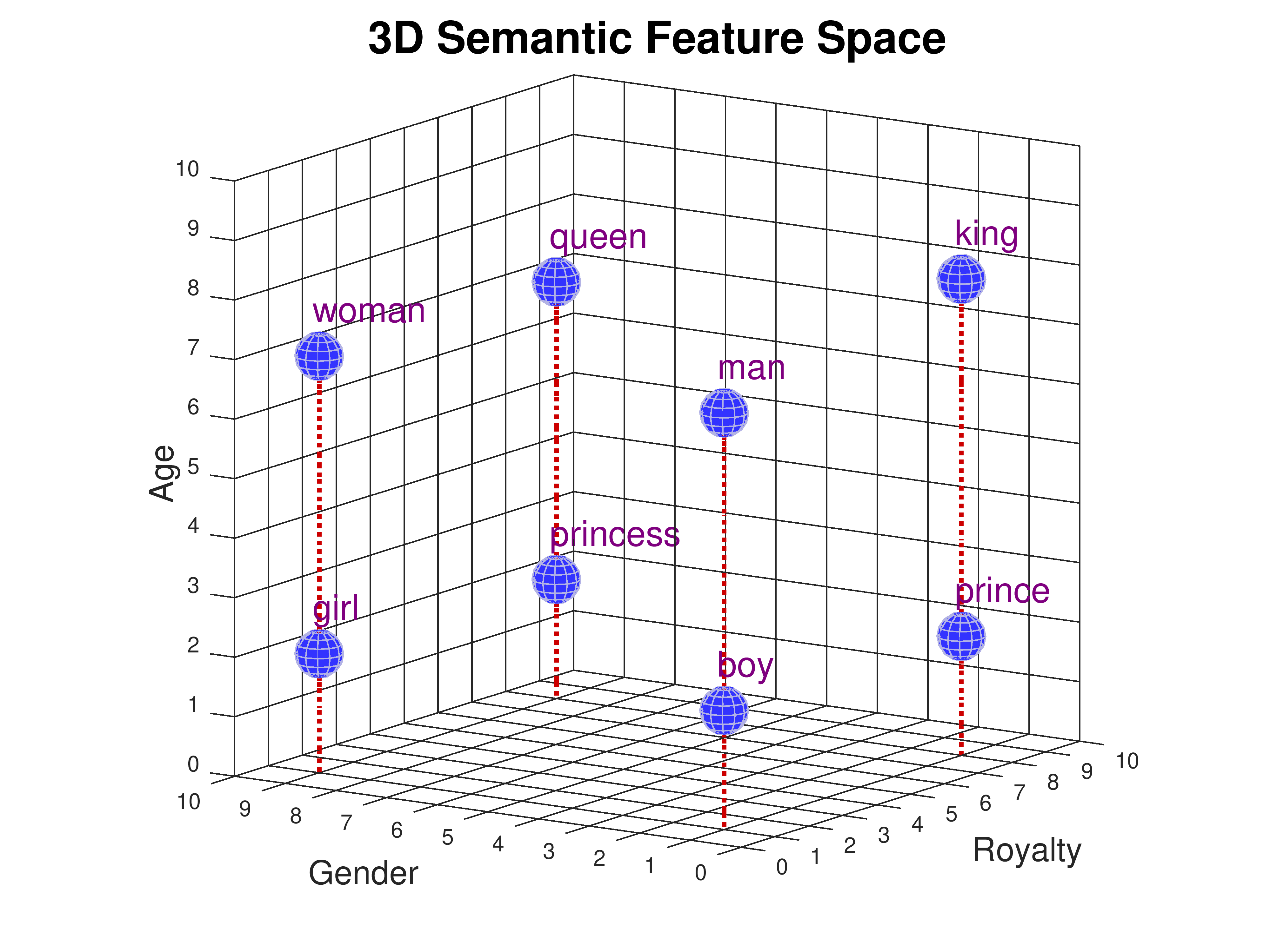
图 19 词嵌入的示意图(图片来源：CMU : Word Embedding Demo)

\(\hspace{1.5em}\) 从上图中我们可以发现，从年纪、性别、王权等不同的维度，我们可以将不同的词映射到不同的位置。从年纪上来看，Woman、queen、king和man在同一个平面（语义相近）；从性别来看，boy、man、prince和king在同一个平面。这样的好处在于，我们可以通过词向量的相似性来判断两个词之间的语义关系。例如，我们可以通过计算两个词向量的余弦相似度来判断两个词之间的语义关系。以下是几种常用的词嵌入方法：

• One-hot encoding：将每个词表示为一个长度为词表大小的稀疏向量，其中仅一个位置为1，其他位置为0。例如在上述例子中，我们将每个词映射为了一个索引，那么我们可以将这个词对应向量的索引位置设为1，其他位置都设为0。尽管简单，但是当词表很大时，这种方法会导致高维稀疏向量，不利于模型的训练和推理。除此之外，one-hot编码无法捕捉词与词之间的语义关系。

• Word2vec：通过神经网络学习每个词的低维向量表示，使得具有相似语境的词在向量空间中彼此接近。Word2vec包含两种主要模型： CBOW （连续词袋模型）和 Skip-gram ，分别通过上下文预测中心词或通过中心词预测上下文。

⁶大家可以思考一下，如何才能让一个模型能够区分同一个词在不同上下文中的含义？（historical hidden information, masked LM）

• GloVe：通过统计词与词之间的共现信息生成词嵌入，使得词的向量表示既包含全局统计信息，也包含局部的语境特征。GloVe的具体实现细节可以参考 GloVe: Global Vectors for Word Representation 。在使用时，我们可以直接加载预训练的GloVe词嵌入，该方式与词元化相似，输入一个词，便能得到一个词向量（在词元化中，我们得到的是一个索引）。这样做的好处是，我们可以直接使用预训练的词嵌入，而无需自己训练模型。但是，这样的缺点在于我们无法利用上下文信息。例如，对于同一个词，它在不同的上下文中可能有不同的含义，而GloVe无法区分这些不同的含义 ^{6 6}大家可以思考一下，如何才能让一个模型能够区分同一个词在不同上下文中的含义？（historical hidden information, masked LM）。

语言模型

\(\hspace{1.5em}\) 在上一节中，我们介绍了处理非结构化文本数据的一些基本术语和预处理方法。那么，当我们得到文本数据的词嵌入后，如何利用这些词向量中的信息对文本数据进行建模呢？这里我们首先介绍 语言模型 （Language Model）的概念。假设长度为 \(n\) 的文本序列为 \(w_1, w_2, \dots, w_n \in \mathcal{R}^{d_e}\)，其中 \(d_e\) 是词嵌入的维度。语言模型的目标是从概率的角度去理解文本。例如，可以通过计算文本中词语出现的联合概率，\(P(w_1, w_2, \dots, w_n)\) ，来评估文本的合理性，文本越合理，则联合概率越高。在“人咬狗”和“狗咬人”这两句话中，后者更符合常识，因此在一个优秀的语言模型中，后者的概率会更高。

联合概率的计算

\(\hspace{1.5em}\) 在本例中，假设 \(w_1 = \text{人}\)， \(w_2 = \text{咬}\)， \(w_3 = \text{狗}\)。虽然从概率角度来说，\(P(w_1, w_2, w_3) = P(w_3, w_2, w_1)\)，但是在语言模型中，这两个概率实际上是不等的。这是因为词语之间并不是 独立 的，因此我们在计算联合概率的时候，其实是在计算条件概率的乘积。例如，\(P(w_1, w_2, w_3) = P(w_1)P(w_2|w_1)P(w_3|w_1, w_2)\)，而 \(P(w_3, w_2, w_1) = P(w_3)P(w_2|w_3)P(w_1|w_3, w_2)\)。从这里我们可以看到，在语言模型中，词元之间的 顺序 其实隐含在了条件概率中。

\(\hspace{1.5em}\) 而文本生成可以看作一个条件概率问题，模型通过条件概率预测下一个词的可能性：

\[P(w_{n+1} | w_1, w_2, \dots, w_n).\]

\(\hspace{1.5em}\) 通过对这个条件概率的计算，我们可以预测文本中的下一个词，进而生成连贯的句子。近年来，大型语言模型（Large Language Model, LLM）如 ChatGPT 备受关注，其核心正是基于语言模型。例如，使用相同输入在 ChatGPT 中常会得到不同的答案：

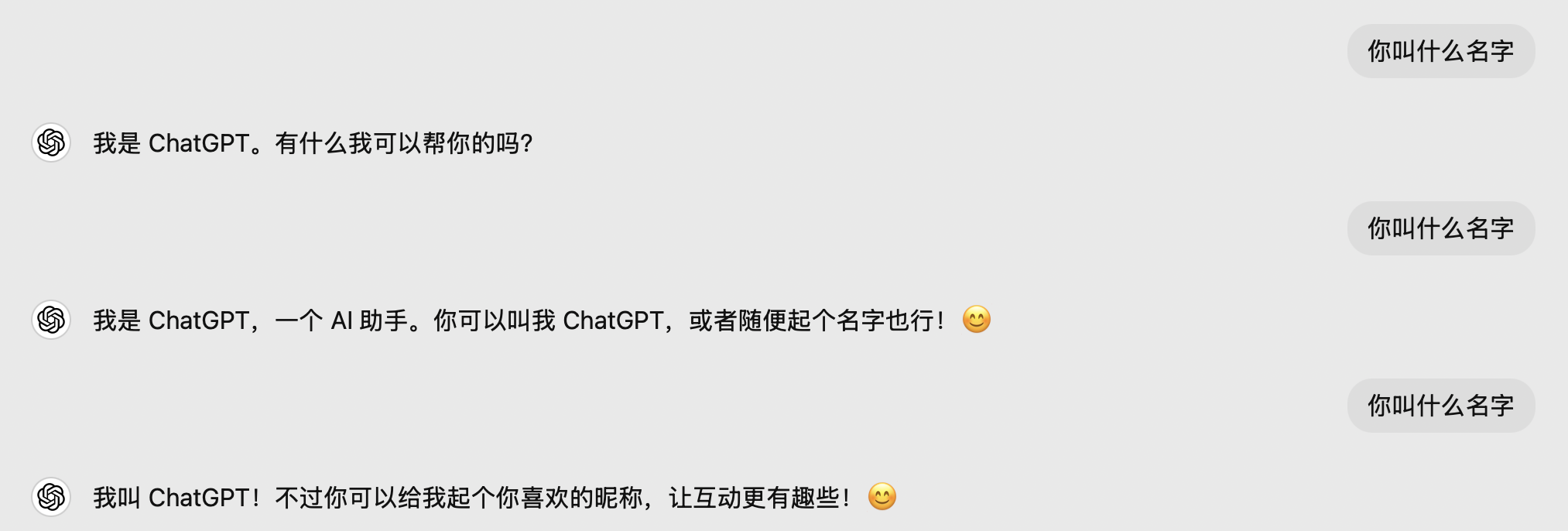
图 20 输入同一句话，得到不同的答案

\(\hspace{1.5em}\) ChatGPT 在生成文本时，实际上是在计算给定上下文中下一个词的概率分布。通过采样下一个词，将其加入上下文后继续生成，直到生成完整的句子 ^{7 7}通常来说，当模型采样出 <EOS> (end of sequence)时，生成的句子就结束了。。因此，相同的输入会产生不同的输出。以下是语言模型的一些主要应用：

1. 文本生成 ：语言模型能够生成自然流畅的文本，广泛应用于内容创作、写作辅助和新闻摘要等场景。像GPT系列这样的模型可以基于输入主题自动创作相关段落，使创作更轻松高效。

2. 下一个词预测 ：语言模型能够根据已有上下文预测可能出现的下一个词，用于自动补全和输入法预测。例如，手机的自动输入建议为用户提供更快捷的输入体验。

3. 机器翻译 ：语言模型在机器翻译中实现语言间的转化，基于Transformer的模型（如Google翻译和DeepL）能够在保持上下文连贯性的同时捕捉句子深层语义，使译文更贴近自然语言表达。

4. 情感分析 ：通过识别词和词组的情感倾向，语言模型可以判断评论、社交媒体帖子和产品反馈等文本的情感倾向（如正面、负面或中立），为市场分析和舆情监测提供支持。

5. 问答系统 ：语言模型在智能问答和对话机器人（如ChatGPT）中提供精准回答、生成互动对话，甚至能够记忆上下文，从而实现更自然、更具互动性的交流体验。

\(\hspace{1.5em}\) 在后续的章节中，我们将探讨如何利用不同类型的语言模型（如循环神经网络、LSTM、Transformer）来处理复杂的文本数据。

⁸“循环神经网络（Recurrent Neural Networks， RNNs）”泛指一类模型，这些模型具有相同的循环结构，区别在于每个模型的循环单元（Cell structure）不同；而“循环神经网络（Recurrent Neural Network， RNN）”通常特指最基本的循环神经网络模型（Vanilla RNN）。在本章中，我们统一用循环神经网络代表这一类模型，而用RNN特指Vanilla RNN模型。

循环神经网络（Recurrent Neural Networks, RNNs） ^{8 8}“循环神经网络（Recurrent Neural Networks， RNNs）”泛指一类模型，这些模型具有相同的循环结构，区别在于每个模型的循环单元（Cell structure）不同；而“循环神经网络（Recurrent Neural Network， RNN）”通常特指最基本的循环神经网络模型（Vanilla RNN）。在本章中，我们统一用循环神经网络代表这一类模型，而用RNN特指Vanilla RNN模型。

\(\hspace{1.5em}\) 在引言中，我们认识到，选择合适的模型在数据建模过程中至关重要。对于静态数据（如图像和表格数据），由于不涉及时间顺序，可以使用多层感知机（MLP）或卷积神经网络（CNN）进行建模。然而，对于序列数据而言，输入数据的顺序尤为重要。例如在时间序列数据（如股票价格、气象数据）和文本数据（如句子、对话）中，当前观测值通常与历史观测值密切相关。接下来，我们将以时间序列预测和语言模型这两个经典问题为切入点，去理解循环神经网络（RNN）的基本思想和原理。

\(\hspace{1.5em}\) 如何才能让神经网络有效地对序列数据进行建模呢？从前两节内容中我们可以看出，序列数据的核心特征是“ 时间依赖性 ”，即输出不仅依赖于当前的输入，还与历史数据密切相关。在前面讨论中我们提到，从线性回归模型发展到自回归模型的关键转变在于，将滞后阶变量（lagged variables）作为自变量引入模型。此外，许多序列数据还具备一个重要性质，即马尔可夫性质：当前观测值仅与前一个或前几个观测值相关。也就是说，\(P(x_t | x_{t-1}, ..., x_{1}) = P(x_t | x_{t-1})\) 或者 \(P(x_t | x_{t-1}, ..., x_{1}) = P(x_t | x_{t-1}, x_{t-2}, ..., x_{t-P})\)。基于此，一个简单的想法是，像自回归模型一样，将前 \(P\) 个观测值输入神经网络中，以便输出预测值 \(\hat x_t\)，从而让网络“利用”历史信息来更好地捕捉序列数据中的时间相依性。

\(\hspace{1.5em}\) 然而，这种方法存在多个问题：

1. 模型是否满足马尔可夫性？模型满足几阶马尔可夫性？也就是说，我们无法确定模型的滞后阶数（即需要考虑多少个历史观测值）。

2. 模型参数数量会随滞后阶数的增加而增长，导致模型复杂度和训练难度显著增加。

3. 由于MLP的输入维度是固定的，因此无法处理变长的序列数据。

\(\hspace{1.5em}\) 有没有更好的方法呢？回到问题的本质，我们希望能保留和利用历史信息。然而，历史信息本质上是一个难以精确捕捉的概念。最理想的历史信息当然是所有真实的历史观测值，但直接将这些信息输入神经网络是不现实的。为此，研究者们引入了一个巧妙的替代方案：用一个隐藏状态（hidden state）来近似历史信息。即

\[P(x_t | x_{t-1}, ..., x_{1}) \approx P(x_t | h_{t-1}).\]

\(\hspace{1.5em}\) 从直观上看，我们可以将隐藏状态视为历史信息在一个不可直接观测的空间（latent space）中的抽象表达。在每个时刻 \(t\)，神经网络接收当前输入 \(x_t\) 和前一时刻的隐藏状态 \(h_{t-1}\)，其中 \(h_{t-1}\) 包含了时刻 \(t\) 之前所有的历史信息。数据经过神经网络后，我们得到最新的隐藏状态 \(h_t\)，该隐藏状态在 \(h_{t-1}\) 的基础上增加了 \(x_t\) 的信息。通过这种方式，我们便可以不断对历史信息进行保留（利用）和更新。

\(\hspace{1.5em}\) 接下来，我们给出 RNNs 的基本结构：

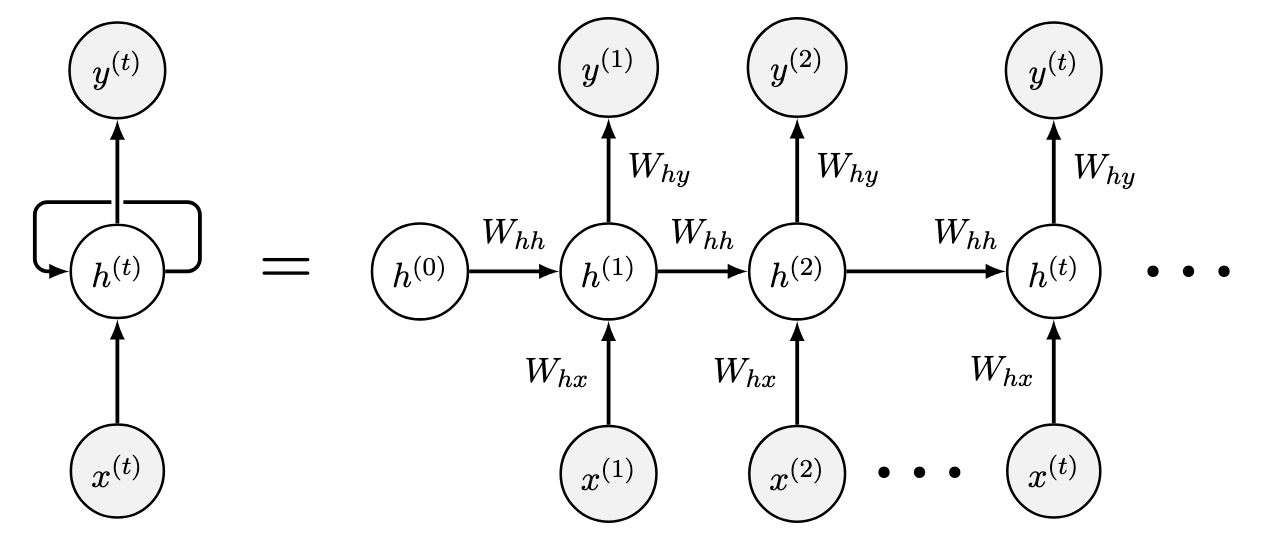
图 21 Vanilla RNN的基本结构

\(\hspace{1.5em}\) 图中左侧部分展示了 RNNs 的基本结构，其中 \(h_t\) 部分为循环单元（recurrent unit or cell unit），通过结合当前时刻输入与前一时刻的隐藏状态，对当前时刻的隐藏状态进行更新。这个反馈结构使得历史信息能够逐步传递到当前时刻，避免了模型定阶的问题。上图右侧部分展示了模型在时间步 \(t\) 的具体更新过程。对于所有 RNNs 来说，这个反馈结构都是相同的，不同点在于循环单元的具体形式。在 Vanilla RNN 中，循环单元的更新方程如下：

(41)\[\begin{split}h_t &= \tanh(W_{hh} h_{t-1} + W_{{hx}} x_t + b_h)\\ y_t &= \sigma(W_{{yh}} h_t + b_y).\end{split}\]

更新方程 () 描述了RNN在时刻 \(t\) 的计算过程。设输入、输出和隐藏状态的维度分别为 \(d_i, d_o, d_h\)，其中输入 \(x_t \in \mathcal{R}^{d_i}\)，输出 \(y_t \in \mathcal{R}^{d_o}\)，隐藏状态 \(h_t \in \mathcal{R}^{d_h}\)。模型的权重矩阵为 \(W_{hh} \in \mathcal{R}^{d_h \times d_h}\)、\(W_{hx} \in \mathcal{R}^{d_h \times d_i}\) 和 \(W_{yh} \in \mathcal{R}^{d_o \times d_h}\)，偏置项为 \(b_h \in \mathcal{R}^{d_h}\) 和 \(b_y \in \mathcal{R}^{d_o}\)。在时刻 \(t\)，模型的输入包含当前输入 \(x_t\) 和前一时刻的隐藏状态 \(h_{t-1}\)。这种设计使得历史信息能够逐步传递至当前时刻，从而对隐藏状态进行更新得到 \(h_t\)。更新后的隐藏状态 \(h_t\) 可以看作是历史信息的加总，对其进行非线性变化后得到当前时刻的输出 \(y_t\)。

RNNs中的单元结构

\(\hspace{1.5em}\) RNNs中的单元结构（Cell）类似于一个只接收单个训练样本的多层感知机（MLP），并且每一个时刻的MLP使用 相同的权重矩阵 （参数共享）。与普通MLP的不同之处在于，RNNs拥有反馈循环，这使得信息可以在时间序列中得以传递和保留。针对RNN单元的前向传播和反向传播，可以参考第一章（单一隐藏层神经网络--基于一个样本点）的内容。

\(\hspace{1.5em}\) 为了让大家更清楚的理解Vanilla RNN的工作原理，我们可以动手写一个 RNN Cell 类 ^{9 9}在 RNN Cell 中，我们只需要考虑隐藏状态 \(h_t\) 的更新，而不需要考虑输出 \(y_t\) 的计算。：

   import torch
   import torch.nn as nn

   class RNN_Cell(nn.Module):
      def __init__(self, input_size, hidden_size):
         super(RNN_Cell, self).__init__()
         self.hidden_size = hidden_size
         self.input_size = input_size
         # h_t = \tanh(W_{hh} h_{t-1} + W_{{hx}} x_t + b_h)
         # nn.Linear中包括了W_{hh}, W_{{hx}}和b_h
         self.i2h = nn.Linear(input_size + hidden_size, hidden_size)

      # input是一个时间步的输入: [input_size]
      def forward(self, input, hidden):
         if hidden is None:
            hidden = torch.zeros(self.hidden_size)
         # Cell里的input只是一个时间步的输入
         # 将输入x_t和隐藏状态h_{t-1}拼接在一起
         combined = torch.cat((input, hidden), 1)
         # 得到h_t
         hidden = self.i2h(combined)
         return hidden

\(\hspace{1.5em}\) 在 RNN Cell 类中，我们定义了每一个时间步下，如何更新隐藏状态。而在 RNN 类中，我们需要对每一个时间步都调用 RNN Cell 类来更新隐藏状态。下面是一个简单的 RNN 类的实现：

   import torch
   import torch.nn as nn
   class RNN(nn.Module):
      def __init__(self, input_size, hidden_size, output_size):
         super(RNN, self).__init__()
         self.hidden_size = hidden_size
         self.rnn = RNN_Cell(input_size, hidden_size)
         self.output = nn.Linear(hidden_size, output_size)

      # input是整个序列: [seq_len, input_size]
      def forward(self, input, hidden):
         # 初始化隐藏状态
         if hidden is None:
            hidden = torch.zeros(self.hidden_size)
         # 对于RNN来说，时间步等于序列长度
         for i in range(input.size(0)):
            # 对每一个时间步，使用RNN_Cell更新隐藏状态
            # h_i = RNN_Cell(x_i, h_{i-1})
            # python语法中，hidden会被更新
            hidden = self.rnn(input[i], hidden)
         # 得到最终的隐藏状态，通过全连接层得到输出
         y_t = self.output(hidden)
         return y_t

\(\hspace{1.5em}\) 通过将每一步计算隐藏状态的过程封装在 RNN Cell 类中，我们可以更清晰地理解RNN的工作原理。对于其他类型的 RNN（如 LSTM 和 GRU），唯一的区别在于 Cell 类的具体结构，而整个 RNN 类的框架是相似的 ^{10 10}RNN Cell 仅返回当前时间步 \(t\) 的隐藏状态，因此在 RNN 中只需处理这个状态。然而，对于即将介绍的 LSTM Cell，不仅会返回隐藏状态，还会返回一个单元状态（Cell state），因此在 LSTM 中需要同时考虑这两个状态。除此之外，RNN 和 LSTM 的基本框架几乎相同。。

\(\hspace{1.5em}\) 在循环神经网络中，每个时刻 \(t\) 我们会输入一个 \(x_t\)，对应会得到一个更新后的隐藏状态 \(h_t\) 和输出 \(\hat y_t\)。根据目标任务的不同，我们会有不同的架构（architecture）用于计算损失函数、训练模型。下面我们介绍3种架构：

1. 堆叠架构（stacked architecture）：顾名思义，是将多个RNN堆叠在一起。在堆叠架构中，每一层的隐藏状态都会作为下一层的输入。这种架构可以帮助模型更好地捕捉序列数据中的复杂关系，提高模型的表达能力。下图展示了堆叠架构的示意图：

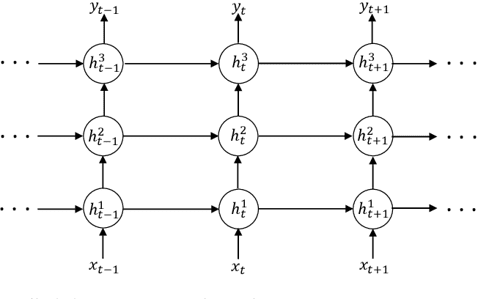
图 22 堆叠架构的示意图

¹¹在文本分析中，双向RNN能有效利用上下文信息。其中，上文信息通过正向RNN传递，下文信息通过反向RNN传递。这种架构能够更好地捕捉文本中的语义关系。

2. 双向架构（bidirectional architecture）：在双向架构中，我们会有两个RNN，一个是正向RNN，一个是反向RNN。正向RNN会接收输入序列，然后从左到右计算隐藏状态；反向RNN会接收输入序列，然后从右到左计算隐藏状态。最后，我们会将两个RNN的隐藏状态拼接（concatenate）在一起，然后通过一个全连接层来计算输出。这种架构在序列标注、情感分析等任务中非常有效 ^{11 11}在文本分析中，双向RNN能有效利用上下文信息。其中，上文信息通过正向RNN传递，下文信息通过反向RNN传递。这种架构能够更好地捕捉文本中的语义关系。。下图展示了双向架构的示意图：

图 23 双向RNN的示意图（图片来源： Wikipedia）

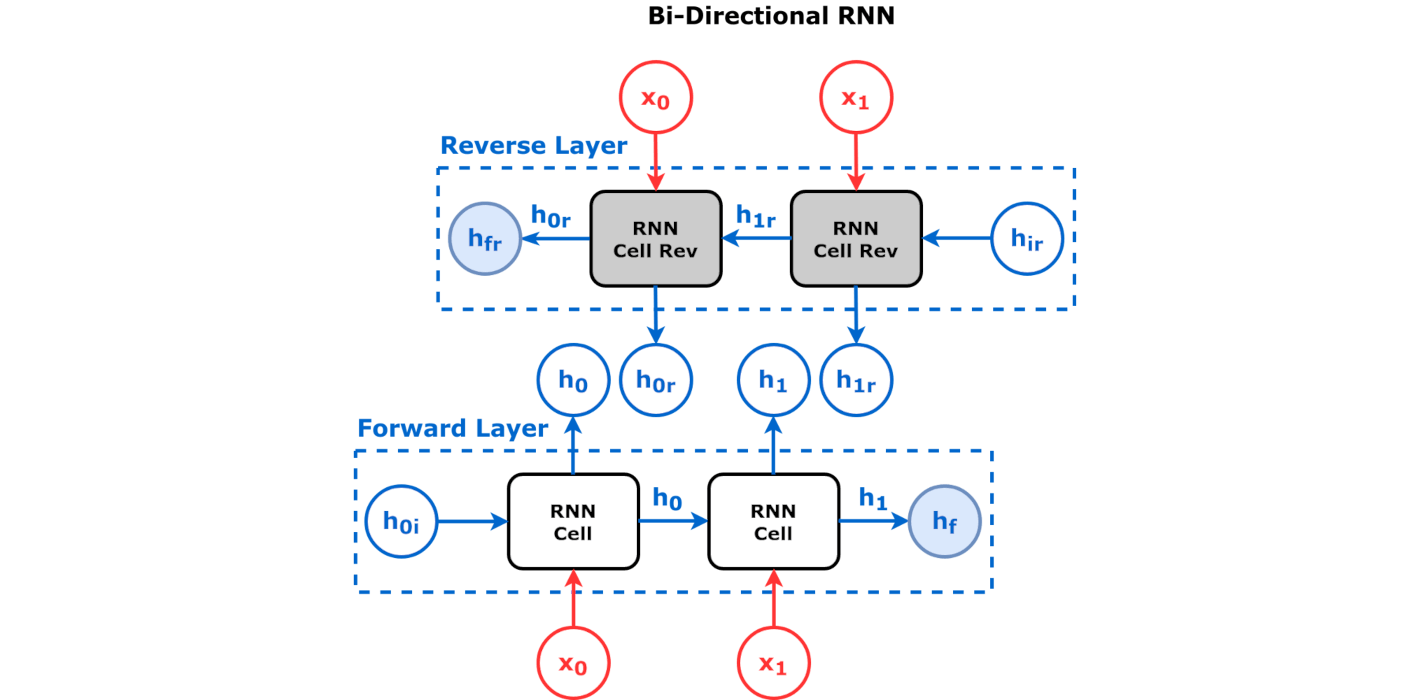
3. 序列到序列（seq2seq）：我们会有两个RNN，一个是编码器（encoder），一个是解码器（decoder）。编码器会接收输入序列，然后将序列的信息编码到一个固定长度的向量中，该向量可以看作是对整个序列的压缩。解码器会接收编码器的输出，然后根据这个输出来生成目标序列。这种架构在机器翻译、文本摘要等任务中非常有效。下图展示了seq2seq架构的示意图：

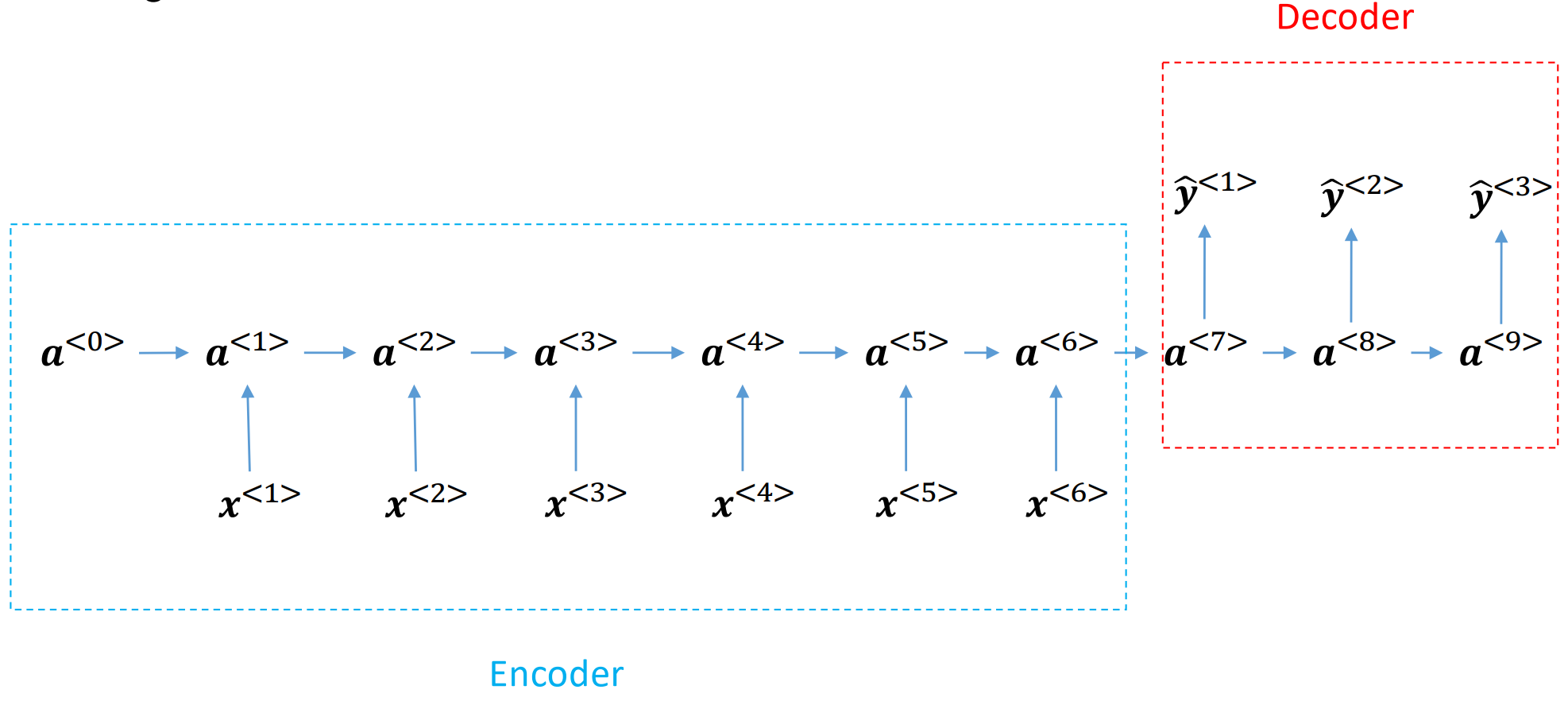
图 24 seq2seq架构的示意图

实际应用中如何选择模型架构

\(\hspace{1.5em}\) 在实际应用中，堆叠式架构因其层级设计与时间序列中的自回归模型类似，常被用于时间序列预测。这种架构通过多层网络逐步提炼特征，能够捕捉复杂的时间依赖关系，从而提升预测性能。

\(\hspace{1.5em}\) 此外，双向架构和seq2seq架构在文本和语音分析中尤为常见。双向架构通过同时考虑前后文信息，生成更加全面的特征表示，因此在自然语言处理（NLP）任务（如命名实体识别、机器翻译和语音识别）中表现出色seq2seq架构则以其灵活性成为机器翻译、文本摘要和问答系统等任务的核心方法。在seq2seq架构中，编码器和解码器的设计可以根据任务需求灵活调整。例如，编码器可以采用双向架构以充分捕捉输入序列的上下文信息，解码器则可以使用传统的单向架构或更复杂的模型（如 Transformer），以增强对长距离依赖的处理能力。此外，还可以结合其他模型（如卷积神经网络或预训练语言模型）来进一步提升性能。这种灵活的模块化设计使seq2seq架构在适配不同应用场景时，能够保持较高的性能和泛化能力。

\(\hspace{1.5em}\) 下面，我们以模拟生成的自回归AR(1)过程为例，举例说明如何用RNN对序列数据进行建模（in-sample fitting）。

import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt

# 模拟生成AR(1)过程
def generate_AR1_data(n, phi):
   x = np.zeros(n)
   for i in range(1, n):
      x[i] = phi * x[i-1] + np.random.normal(0, 1)
   return x

# 生成数据
n = 1000
phi = 0.8
x = generate_AR1_data(n, phi)

# 数据预处理
x = torch.tensor(x, dtype=torch.float32).view(-1, 1)
# 在时间序列预测中，y_t = x_{t+1}
# 所以我们的输入是 x_0, x_1, ..., x_998
# 我们的输出（target）是 x_1, x_2, ..., x_999
y = x[1:]
x = x[:-1]

# 定义RNN模型
class RNN(nn.Module):
   def __init__(self, input_size, hidden_size, output_size):
      super(RNN, self).__init__()
      self.hidden_size = hidden_size
      # 使用torch中的RNN，这里也可以换成之前我们自己写的RNN类
      # 后面我们会看到，这里我们还可以使用nn.LSTM或者nn.GRU
      # bidirectional=False表示单向RNN，为True时表示双向RNN
      # num_layers=1表示RNN的层数为1，对应stacked architecture中的层数
      self.rnn = nn.RNN(input_size, hidden_size, num_layers=1, bidirectional=False, batch_first=True)
      self.output = nn.Linear(hidden_size, output_size)

   def forward(self, x, hidden):
      # 请查阅pytorch官方文档，弄明白nn.RNN的输出是什么，有什么参数
      y, hidden = self.rnn(x, hidden)
      # 输出层
      y = self.output(y)
      return y, hidden

# 训练模型
input_size = 1
hidden_size = 32
output_size = 1
model = RNN(input_size, hidden_size, output_size)
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)

model.train()
for epoch in range(100):
   hidden = None
   optimizer.zero_grad()
   y_pred, hidden = model(x.view(1, -1, 1), hidden)
   loss = criterion(y_pred.view(-1), y.view(-1))
   loss.backward()
   optimizer.step()

# 预测
model.eval()
hidden = None
y_pred, _ = model(x.view(1, -1, 1), hidden)

# 可视化
plt.plot(y.detach().numpy(), label='True')
# detach是将y_pred从计算图中分离出来，不再计算梯度
plt.plot(y_pred.detach().numpy().flatten(), label='Predicted')
plt.legend()
plt.show()

\(\hspace{1.5em}\) 最后模型输出如下图片 ^{12 12}在本例中，我们将所有数据都当作了训练数据，因此模型会出现过拟合（overfitting）的问题。在实际应用中，我们需要将数据分为训练集（参数估计，in-sample fitting）、验证集（选择额超参数，hyper-parameters tuning）和测试集（样本外预测，out-sample forecasting），以便评估模型的泛化能力。：

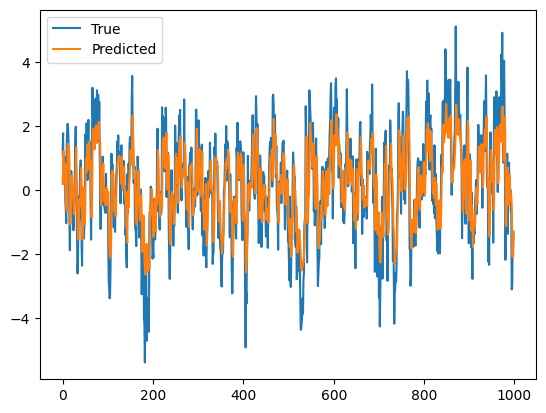
图 25 使用RNN对AR(1)过程进行预测

\(\hspace{1.5em}\) 为了研究梯度在RNN中是如何传播的，我们考虑一个简单的RNN模型。忽略激活函数和误差项 ^{13 13}为了更清楚直观的解释BPTT的原理，不失一般性地，我们假设激活函数为 identity 函数，即 \(\sigma(x) = x\)，偏置项为0。针对更一般的激活函数（如 \(tanh(\cdot)\) 等），只需在反向传播过程中乘上一项激活函数的导数即可。，我们可以将RNN的前向传播过程表示如下：

(42)\[\begin{split}h_0 &= 0 \\ h_1 &= W_{hh} h_0 + W_{hx} x_1, \hat y_1 = W_{yh} h_1 \\ h_2 &= W_{hh} h_1 + W_{hx} x_2, \hat y_2 = W_{yh} h_2 \\ h_3 &= W_{hh} h_2 + W_{hx} x_3, \hat y_3 = W_{yh} h_3 \\ &\dots \\ h_T &= W_{hh} h_{T-1} + W_{hx} x_T, \hat y_T = W_{yh} h_T,\end{split}\]

其中，\(W_{hh}\) 、\(W_{hx}\) 、\(W_{yh}\) 是权重矩阵，也是我们需要训练的参数。为了使用梯度下降法来训练RNN，我们需要计算损失函数对权重矩阵的梯度。以均方误差作为损失函数（loss function），我们可以得到：

\[\mathcal{J} = \frac{1}{T} \sum_{t=1}^{T} (y_t - \hat y_t)^2,\]

其中，\(\mathcal{J}\) 是损失函数（cost function），\(T\) 是序列的长度。为了更新权重矩阵，我们需要计算 \(\frac{\partial \mathcal{J}}{\partial W_{hh}}\)、\(\frac{\partial \mathcal{J}}{\partial W_{hx}}\) 和 \(\frac{\partial \mathcal{J}}{\partial W_{yh}}\)。首先，我们给出一个简单的前向传播的示意图，并逐步分析RNN如何通过链式法则计算梯度：

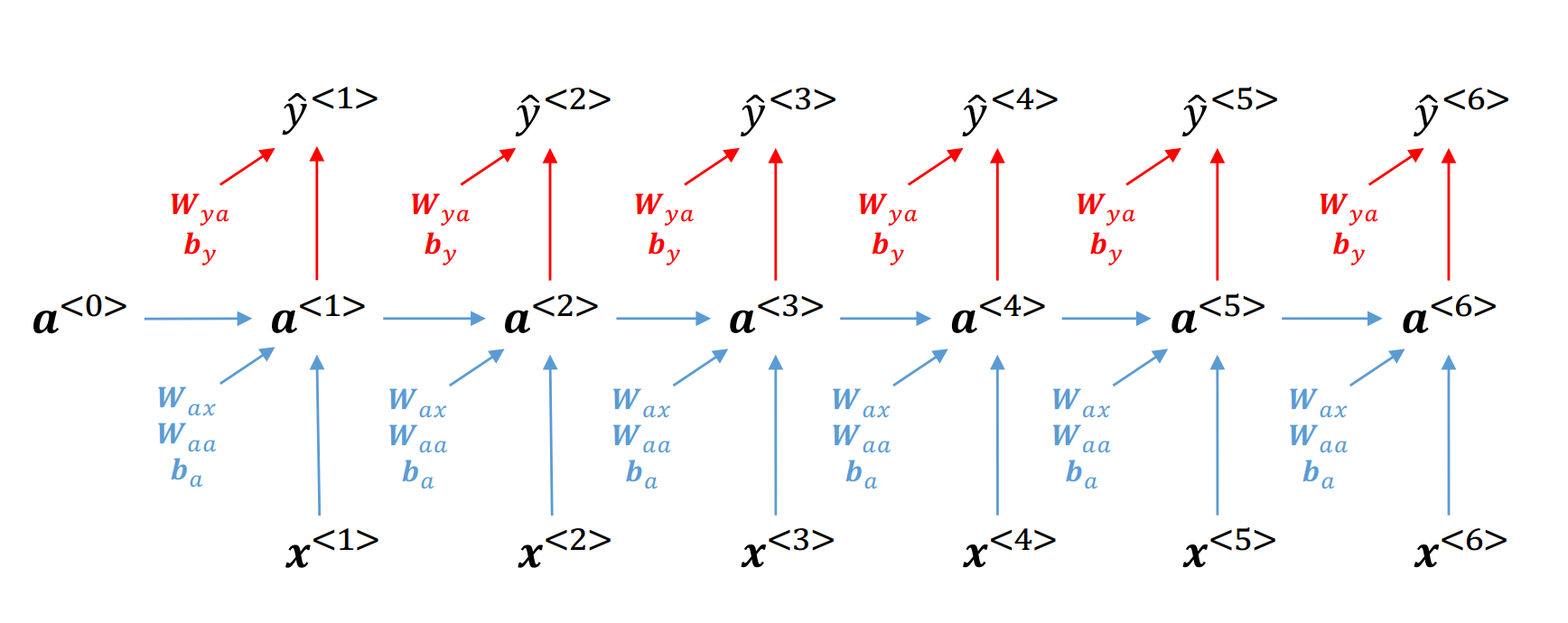
图 26 RNN的前向传播示意图

\(\hspace{1.5em}\) 对于 \(W_{yh}\)，我们可以发现每个时刻 \(t\) 都存在一条 \(\mathcal{J} \to \hat y_t \to W_{yh}\) 的路径。因此，我们可以直接计算梯度：

\[\begin{split}\frac{\partial \mathcal{J}}{\partial W_{yh}} &= \sum_{t=1}^{T} \frac{\partial \mathcal{J}}{\partial \hat y_t} \frac{\partial \hat y_t}{\partial W_{yh}} \\ &= \sum_{t=1}^{T} - \frac{2}{T} (y_t - \hat y_t) (h_t)^{\top}.\end{split}\]

\(\hspace{1.5em}\) 对于 \(W_{hh}\) 和 \(W_{hx}\)，在计算梯度时我们需要考虑未来时刻的梯度如何反向传播到当前时刻。在上图中，以时刻 \(3\) 的 \(W_{hh}\) 为例，会有多条路径从 \(\mathcal{J}\) 到 \(W_{hh}\)。这些路径包括：

(43)\[\begin{split}\mathcal{J} \to \hat y_3 \to h_3 &\to W_{hh} \\ \mathcal{J} \to \hat y_4 \to h_4 \to h_3 &\to W_{hh} \\ \mathcal{J} \to \hat y_5 \to h_5 \to h_4 \to h_3 &\to W_{hh} \\ \mathcal{J} \to \hat y_{6} \to h_{6} \to \dots \to h_3 &\to W_{hh}.\end{split}\]

\(\hspace{1.5em}\) 为了简化计算，我们考虑如下简化的路径：\(\mathcal{J} \to (\cdot) \to h_t \to W_{hx}/W_{yh}\)，其中 \((\cdot)\) 代表了所有可能的路径。因此，我们可以将链式法则表示为：

\[\begin{split}\frac{\partial \mathcal{J}}{\partial W_{hh}} &= \sum_{i=1}^{T} \frac{\partial \mathcal{J}}{\partial \hat h_{i}} \frac{\partial \hat h_{i}}{\partial W_{hh}} \\ \frac{\partial \mathcal{J}}{\partial W_{hx}} &= \sum_{i=1}^{T} \frac{\partial \mathcal{J}}{\partial \hat h_{i}} \frac{\partial \hat h_{i}}{\partial W_{hx}}.\end{split}\]

\(\hspace{1.5em}\) 这样做的好处在于，路径 \(h_t \to W_{hx}/W_{hh}\) 的梯度是容易算的，我们只需要弄清楚 \(\mathcal{J} \to (\cdot) \to h_t\) 这一部分的梯度即可。由 () 我们可以推出时刻 \(t\) 时 \(\mathcal{J} \to (\cdot) \to h_t\) 可以取以下路径：

\[\begin{split}\mathcal{J}& \to \hat y_t & \to h_t \\ \mathcal{J}& \to \hat y_{t+1} \to h_{t+1} & \to h_t \\ \mathcal{J}& \to \hat y_{t+2} \to h_{t+2} \to h_{t+1} & \to h_t \\ &\vdots \\ \mathcal{J}& \to \hat y_{T} \to h_{T} \to \dots \to h_{t+1} & \to h_t.\end{split}\]

\(\hspace{1.5em}\) 因此，在计算 \(\frac{\partial \mathcal{J}}{\partial h_t}\) 时，我们会得到如下结果：

(44)\[\begin{split}\frac{\partial \mathcal{J}}{\partial h_t} &= \sum_{\tau = t}^{T} \frac{\partial \mathcal{J}}{\partial \hat y_{\tau}} \frac{\partial \hat y_{\tau}}{\partial h_{\tau}} (\Pi_{i=t+1}^{\tau} \frac{\partial h_{i}}{\partial h_{i-1}}) \\ &= - \frac{2}{T} \sum_{\tau = t}^{T} {\color{red}{(W_{hh}^{\top})^{\tau - t}}} W_{yh}^{\top} (y_{T + t - \tau} - \hat y_{T + t - \tau}).\end{split}\]

RNN中的梯度消失/爆炸

\(\hspace{1.5em}\) 由 () 我们可以看到，从 \(\mathcal{J} \to \hat y_{\tau} \to h_{\tau} \to \dots \to h_{t+1} \to h_t\) 这条路径反向传播的梯度，梯度的大小与 \((W_{hh}^{\top})^{\tau - t}\) 有关。当 \(\tau \gg t\) 时，如果 \(\|W_{hh}\| > 1\)，梯度会出现NaN（梯度爆炸），导致模型参数无法更新；如果 \(\|W_{hh}\| < 1\)，梯度会趋于0（梯度消失）。因为有多条路径反向传播，在梯度消失时，近距离的梯度成为主项（dominant），因此模型无法利用远距离（\(\tau \gg t\)）的梯度。此时，在每一个时刻 \(t\)，模型只能学习到近距离的信息，而无法学习长距离的依赖关系（long-term dependence）。

\(\hspace{1.5em}\) 最后，应用链式法则，我们可以得到：

\[ \begin{align}\begin{aligned}\begin{split}\frac{\partial \mathcal{J}}{\partial W_{hh}} &= \sum_{t = 1}^{T} \frac{\partial \mathcal{J}}{\partial h_t} \frac{\partial \hat h_{i}}{\partial W_{hh}} \\ &= \sum_{t = 1}^{T} \frac{\partial \mathcal{J}}{\partial h_t} (h_{t-1})^{\top}\end{split}\\\begin{split}\frac{\partial \mathcal{J}}{\partial W_{hx}} &= \sum_{t = 1}^{T} \frac{\partial \mathcal{J}}{\partial h_t} \frac{\partial \hat h_{i}}{\partial W_{hx}} \\ &= \sum_{t = 1}^{T} \frac{\partial \mathcal{J}}{\partial h_t} (x_{t})^{\top},\end{split}\end{aligned}\end{align} \]

其中 \(\frac{\partial \mathcal{J}}{\partial h_t}\) 由 () 给出。

BPTT的计算

\(\hspace{1.5em}\) 在上述计算中，我们显示的将所有可能的路径写出来然后进行梯度的计算。在实际应用中，我们可以递归的计算梯度 \(\frac{\partial \mathcal{J}}{\partial h_t}\)，这样既简洁又高效。下面我们简要说明一下如何计算。

\(\hspace{1.5em}\) 当 \(t = T\) （最后一步）时，只有一条路径反向传播梯度：

1. \(\mathcal{J} \to \hat y_T \to h_T\)；

\[\frac{\partial \mathcal{J}}{\partial h_T} = \frac{\partial \mathcal{J}}{\partial \hat y_T} \frac{\partial \hat y_T}{\partial h_{T}}.\]

在时刻 \(t < T\) 时，梯度经过两条路径反向传播：

2. \(\mathcal{J} \to \hat y_t \to h_t\)；

3. \(\mathcal{J} \to \dots \to h_{t+1} \to h_t\)。

\[\frac{\partial \mathcal{J}}{\partial h_t} = \frac{\partial \mathcal{J}}{\partial h_{t+1}} \frac{\partial h_{t+1}}{\partial h_{t}} + \frac{\partial \mathcal{J}}{\partial \hat y_t} \frac{\partial \hat y_t}{\partial h_{t}}.\]

\(\hspace{1.5em}\) 利用上述的两个公式，我们便可以递归的计算 \(\frac{\partial \mathcal{J}}{\partial h_t}\)。

循环神经网络的变种

\(\hspace{1.5em}\) 在上一节中，我计算了RNN中梯度的反向传播过程。在时间步 \(t\)，所有 \(\tau > t\) 时刻的梯度会通过各个隐藏状态 \(h_{t + i} (i = \tau, \tau-1, \dots, 1)\) 向 \(h_t\) 反向传播。然而，由于包含连乘项 \((\Pi_{i=t+1}^{\tau} \frac{\partial h_{i}}{\partial h_{i-1}})\)，梯度随着时间步的增加会呈指数级衰减或增长，导致梯度消失或爆炸。为了应对梯度消失问题，Hochreiter和Schmidhuber（1997） 提出了一种利用门控机制（gate mechanism）来控制信息流动的方法。接下来，我们将介绍两种广泛使用的门控循环神经网络变体——长短期记忆网络（LSTM）和门控循环单元（GRU），并解释门控机制如何帮助缓解梯度消失问题。

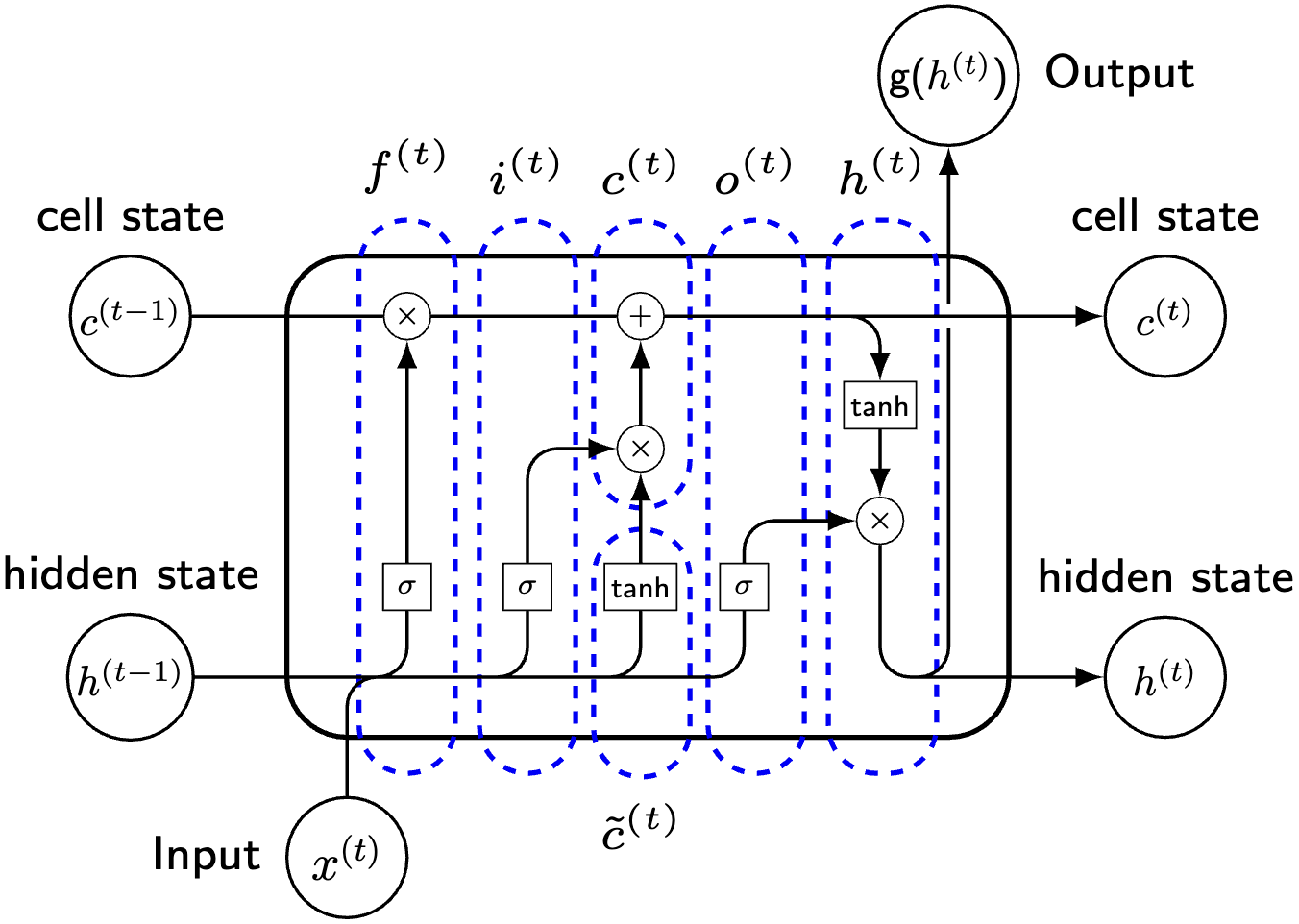
图 27 LSTM单元的基本结构

\(\hspace{1.5em}\) 长短期记忆网络（Long Short-Term Memory，LSTM）是一种特殊的循环神经网络（RNNs），它通过引入三个门控单元来控制信息的流动。LSTM中每个单元的计算公式如下 ^{14 14}这里我们忽略了从隐藏状态 \(h_t\) 到输出 \(y_t\) 的计算，因为这部分和RNN是一样的。在LSTM中，我们主要关注单元状态 \(c_t\) 和隐藏状态 \(h_t\) 的计算。：

\[\begin{split}i_t &= \sigma(W_{ix} x_t + W_{ih} h_{t-1} + b_i) \\ f_t &= \sigma(W_{fx} x_t + W_{fh} h_{t-1} + b_f) \\ o_t &= \sigma(W_{ox} x_t + W_{oh} h_{t-1} + b_o) \\ \tilde c_t &= \tanh(W_{cx} x_t + W_{ch} h_{t-1} + b_c) \\ c_t &= f_t \odot c_{t-1} + i_t \odot \tilde c_t \\ h_t &= o_t \odot \tanh(c_t),\end{split}\]

其中，\(\odot\) 表示 Hadamard 积（逐元素乘积，elementwise product），\(b_i, b_f, b_o, b_c \in \mathcal{R}^{d_h}\) 分别对应于输入门、遗忘门、输出门和单元状态的偏置项。这里，\(d_i\) 和 \(d_h\) 分别表示输入和隐藏状态的维度。通常情况下，\(i_t, f_t, o_t \in \mathcal{R}^{d_h}\) 分别称为输入门、遗忘门和输出门的激活值，\(\tilde c_t \in \mathcal{R}^{d_h}\) 表示候选单元状态，\(c_t \in \mathcal{R}^{d_h}\) 为单元状态，即 LSTM 的内部记忆，而 \(h_t \in \mathcal{R}^{d_h}\) 是LSTM的隐藏状态，也是网络的输出。各权重矩阵和偏置项定义如下：\(W_{ix} \in \mathcal{R}^{d_h \times d_i}\) 和 \(W_{ih} \in \mathcal{R}^{d_h \times d_h}\) 是输入门的权重，\(W_{fx} \in \mathcal{R}^{d_h \times d_i}\) 和 \(W_{fh} \in \mathcal{R}^{d_h \times d_h}\) 是遗忘门的权重，\(W_{ox} \in \mathcal{R}^{d_h \times d_i}\) 和 \(W_{oh} \in \mathcal{R}^{d_h \times d_h}\) 是输出门的权重，\(W_{cx} \in \mathcal{R}^{d_h \times d_i}\) 和 \(W_{ch} \in \mathcal{R}^{d_h \times d_h}\) 是单元状态的权重。

\(\hspace{1.5em}\) 我们首先根据更新方程来理解LSTM的基本构造。首先，LSTM 中的三个门控单元 \(i_t\)、\(f_t\) 和 \(o_t\) 的计算方式是相同的（权重矩阵不同）。每个门控单元通过与输入和前一隐藏状态的线性组合并施加激活函数来得到。这三个向量中每一个元素的值域都在 \((0, 1)\) 之间，因此我们可以将他们看作是权重。

\(\hspace{1.5em}\) 与RNN不同，LSTM中额外增加了一个单元状态（cell state）。从更新方程中我们可以发现，\(\tilde c_t\) 的计算与RNN中隐藏状态的计算方式完全一致，我们可以将LSTM中的候选单元状态与RNN中的隐藏状态作为类比，看作是历史信息的潜在表示。对于单元状态 \(c_t\) 的计算，可以看作是对于历史信息的更新（加权求和）。通过遗忘门 \(f_t\) 控制历史信息 \(c_{t-1}\) 的保留程度，通过输入门 \(i_t\) 控制新信息 \(\tilde c_t\) 的输入。这样的好处在于，在第 \(k\) 个维度，历史信息可以完全保留（ \(f_{t, k} = 1\) ）或者完全遗忘（ \(f_{t, k} = 0\)），新信息可以完全输入（ \(i_{t, k} = 1\) ）或者完全忽略（ \(i_{t, k} = 0\)）。与RNN中隐藏状态的计算相比，LSTM中单元状态的更新多了一步与历史信息的加权求和，这使得LSTM能够更好的保留重要的历史信息。如果我们将 \(\tilde c_t\) 看作是短期记忆（因为仅考虑了 \(h_{t-1}\)），那么 \(c_t\) 可以看作是长期记忆，通过这个加权求和，实现了对历史信息的长期记忆，这也是LSTM名字的由来（Long Short-Term Memory : make the short-term memory long）。

\[\begin{split}\tilde c_t &= \tanh(W_{cx} x_t + W_{ch} h_{t-1} + b_c) \\ c_t &= f_t \odot c_{t-1} + i_t \odot \tilde{c}_t\end{split}\]

\(\hspace{1.5em}\) 在LSTM中，同样使用了一个隐藏状态 \(h_t\)。从 \(h_t\) 的计算方程来看，我们可以将其视作是单元状态 \(c_t\) 的一个可输出表示，这是因为输出门 \(0 < o_{t, k} < 1\) 控制了单元状态的输出到隐藏状态 \(h_t\) 的过程，即从 \(c_t\) 中提取了与输出有关的信息。

\[h_t = o_t \odot \tanh(c_t)\]

图 28 RNN的基本结构

\(\hspace{1.5em}\) 门控循环单元（Gated Recurrent Unit，GRU）是另一种使用了门控机制的循环神经网络（RNNs），它通过引入两个门控单元来控制信息的流动。GRU的计算公式如下：

\[\begin{split}u_t &= \sigma(W_ux x_t + W_uh h_{t-1}) \\ r_t &= \sigma(W_rx x_t + W_rh h_{t-1}) \\ \tilde h_t &= \tanh(W_{hx} x_t + r_t \odot W_{hh} h_{t-1}) \\ h_t &= (1 - u_t) \odot h_{t-1} + u_t \odot \tilde h_t,\end{split}\]

其中 \(u_t \in \mathcal{R}^{d_h}\) 和 \(r_t \in \mathcal{R}^{d_h}\) 分别是更新门和重置门的激活值，\(\tilde h_t \in \mathcal{R}^{d_h}\) 是候选隐藏状态，\(h_t \in \mathcal{R}^{d_h}\) 是隐藏状态；\(W_{ux} \in \mathcal{R}^{d_h \times d_i}\) 和 \(W_{uh} \in \mathcal{R}^{d_h \times d_h}\) 是更新门权重，\(W_{rx} \in \mathcal{R}^{d_h \times d_i}\) 和 \(W_{rh} \in \mathcal{R}^{d_h \times d_h}\) 是重置门权重，\(W_{hx} \in \mathcal{R}^{d_h \times d_i}\) 和 \(W_{hh} \in \mathcal{R}^{d_h \times d_h}\) 是候选隐藏状态的权重。

\(\hspace{1.5em}\) 在GRU中同样使用了门控机制，可以看作是LSTM的一个简化版本。与LSTM不同的是，GRU中只有一个隐藏状态 \(h_t\)，而没有单元状态 \(c_t\)。GRU 的门控机制包含两个门：更新门 \(u_t\) 和重置门 \(r_t\)，它们的计算方式与 LSTM 中的门控单元相似。更新门 \(u_t\) 控制历史信息和新信息的融合比例，而重置门 \(r_t\) 决定历史信息的保留程度。候选隐藏状态 \(\tilde{h}_t\) 则通过前一时刻的历史信息 \(h_{t-1}\) 和当前输入 \(x_t\) 计算得出，其中 \(r_t \odot W_{hh} h_{t-1}\) 可与 LSTM 中的 \(f_t \odot c_{t-1}\) 类比，用于调控历史信息的保留比例。GRU中隐藏状态的计算与LSTM中的隐藏状态计算类似，但是没有了单元状态的概念，因此隐藏状态 \(h_t\) 既是网络的输出，也是网络的内部记忆。

\[\begin{split}\tilde h_t &= \tanh(W_{hx} x_t + r_t \odot W_{hh} h_{t-1}) \\ h_t &= (1 - u_t) \odot h_{t-1} + u_t \odot \tilde h_t\end{split}\]

\(\hspace{1.5em}\) 在RNN中，隐藏状态可以被视为目标序列的潜在表示。LSTM引入了一个单独的单元状态（Cell state）来保存历史信息，它作为时间 \(t\) 前所有信息的摘要。相比之下，GRU直接利用隐藏状态来结合历史信息。这种方法不仅减少了所需的参数数量，例如LSTM中的输出门 \(o_{t}\)，还缓解了将单元状态转换为隐藏状态时产生的偏差（bias）。

\(\hspace{1.5em}\) 除了在表示历史信息方式上的区别，这两种模型在门控机制的使用上也有所不同。例如，LSTM分别使用输入门和遗忘门 \(i_{t}\) 和 \(f_{t}\) 来确定历史信息 \(c_{t-1}\) 与新信息 \(\tilde c_{t}\) 之间的权重。这种方法可能导致当 \(i_{t}\) 和 \(f_{t}\) 取极端值时，单元状态 \(c_{t}\) 变得难以解释 ^{15 15}例如，当 \(i_{t, k} = f_{t, k} = 0 \in \mathcal{R}^{d_h}\) 时，\(c_{t, k} = 0\)。。相比之下，GRU使用更新门 \(u_{t}\) （及其补数 \(\textbf{1} - u_{t}\)）作为权重，确保隐藏状态 \(h_{t}\) 仅由历史信息 \(h_{t-1}\) 和新信息 \(\tilde h_{t}\) 决定。当 \(u_{t, k}\) 接近于0时，表明新信息比历史信息更为重要，且 \(h_{t}\) 完全由 \(\tilde h_{t}\) 决定。然而，鉴于序列建模中的自相关衰减现象，GRU还引入了重置门 \(r_{t}\) 来保留历史信息。该门可以被解释为ARMA模型中的AR系数，功能上类似于LSTM中的遗忘门 \(f_{t}\)。重置门决定了要保留多少历史信息，以生成候选隐藏状态 \(\tilde h_{t}\)。这可以视为一种双重保险，利用了序列中存在的强相关性。

\(\hspace{1.5em}\) 从更新方程上来看，GRU的参数更少，因此计算效率更高。在实际应用中，LSTM和GRU在许多数据集上具有相同的效果（comparable performance）。

\(\hspace{1.5em}\) 在RNN的BPTT中，我们发现，梯度消失或者爆炸主要的原因在于 \(\frac{\partial \mathcal{J}}{\partial h_t}\) 中会出现连乘项 \(\Pi_{i=t+1}^{\tau} \frac{\partial h_{i}}{\partial h_{i-1}}\) 。由于GRU与RNN相同，使用了隐藏状态作为历史信息的潜在表示，同时，GRU和LSTM相比更简单，所以我们以一个简化的GRU模型为例来说明门控机制在BPTT中的作用。

\(\hspace{1.5em}\) 为了简化计算，不失一般性地，我们将激活函数设为 identity 函数：\(\sigma(x) = x\)，同时忽略偏置项。由于GRU中门控单元的计算也会包括 \(x_t\) 和 \(h_{t-1}\)，这会让我们的计算变得复杂。因此，在这里我们考虑门控单元为常数，即 \(u_t = D_u\) 和 \(r_t = D_r\)，其中 \(D_u\) 和 \(D_r\) 是一个对角矩阵，每个对角元素都是常数。这样我们可以将 \(h_t\) 的计算简化为：

(45)\[\begin{split}u_t &= D_u \\ r_t &= D_r \\ \tilde h_t &= W_{hx} x_t + D_r W_{hh} h_{t-1} \\ h_t &= (I - D_u) h_{t-1} + D_u \tilde h_t.\end{split}\]

\(\hspace{1.5em}\) 我们可以对 () 进行进一步化简：

\[\begin{split}h_t &= (I - D_u) h_{t-1} + D_u \tilde h_t\\ &= (I - D_u) h_{t-1} + D_u (W_{hx} x_t + D_r W_{hh} h_{t-1}) \\ &= (I - D_u) h_{t-1} + D_u W_{hx} x_t + D_u D_r W_{hh} h_{t-1} \\\end{split}\]

\(\hspace{1.5em}\) 此时，根据链式法则，我们有：

(46)\[\begin{split}\frac{\partial h_{t}}{\partial h_{t-1}} &= (I - D_u) + D_u D_r W_{hh} \\ &= I - D_u (I - D_r W_{hh}).\end{split}\]

\(\hspace{1.5em}\) 值得注意的是，\(D_u\) 和 \(D_r\) 中对角元素的值域都在 \((0, 1)\) 之间。为了更进一步理解门控机制的作用，我们可以考虑几种极端情况：

1. 当 \(D_u = 0\) 时， \(h_t = h_{t-1}\)，即历史信息完全保留，新信息完全忽略。此时梯度 \(\frac{\partial h_{t}}{\partial h_{t-1}} = I\)，连乘项不会为0；

2. 当 \(D_u = 1, D_r = 0\) 时，\(h_t = \tilde h_t = W_{hx} x_t\)，即历史信息完全忽略，新信息完全保留；此时梯度 \(\frac{\partial h_{t}}{\partial h_{t-1}} = 0\)，由于此时历史信息和未来信息之间没有任何联系，因此梯度（正常）消失；

3. 当 \(D_u = 1, D_r = 1\) 时，\(h_t = W_{hx} x_t + W_{hh} h_{t-1}\)，此时更新方程与RNN相同；

当 \(D_u\) 和 \(D_r\) 的取值在 \((0, 1)\) 之间时，我们可以看到，门控机制 缓解 ^{16 16}虽然LSTM和GRU声称（claim）解决了梯度消失的问题，但实际上只是缓解了这个问题。感兴趣的同学可以参考文章： Do RNN and LSTM have Long Memory? 。 了连乘项 \({\color{red}{(W_{hh}^{\top})^{\tau - t}}}\) 带来的问题。

注意力机制

\(\hspace{1.5em}\) 虽然LSTM和GRU在一定程度上能缓解梯度消失的问题，但当处理很长的序列时，它们仍可能面临信息丢失或记忆不足的困境。比如在机器翻译中，我们常用考虑使用 seq2seq 架构。编码器将输入序列压缩为一个固定长度的向量，作为整个序列的“总结”，然后解码器根据这个向量生成目标序列。这里的问题在于：如果输入的序列非常长，编码器输出的向量往往更偏向序列后部分的信息，而无法全面代表整个序列。此外，在解码器的每一步中，我们使用的上下文信息是相同的，忽视了序列中不同部分的重要性差异。

\(\hspace{1.5em}\) 第一个问题出现的原因是，编码器中的最后一个隐藏状态（last hidden state）并不能很好的代表整个输入序列的信息。那么一个简单的想法是，我将编码器中的所有信息同步输入到解码器中，这样就能充分利用整个输入序列的信息。为了解决第二个问题，我们可以考虑对输入序列的不同部分加入权重，这样就能更好的利用重要的部分信息。上述两者的结合就是注意力机制（attention mechanism）。从这个角度来理解，注意力机制相当于是在编码器和解码器之间添加了一条捷径（shortcuts），用于更好的利用输入序列的信息。

\(\hspace{1.5em}\) 下面，我们给出注意力机制的基本结构：

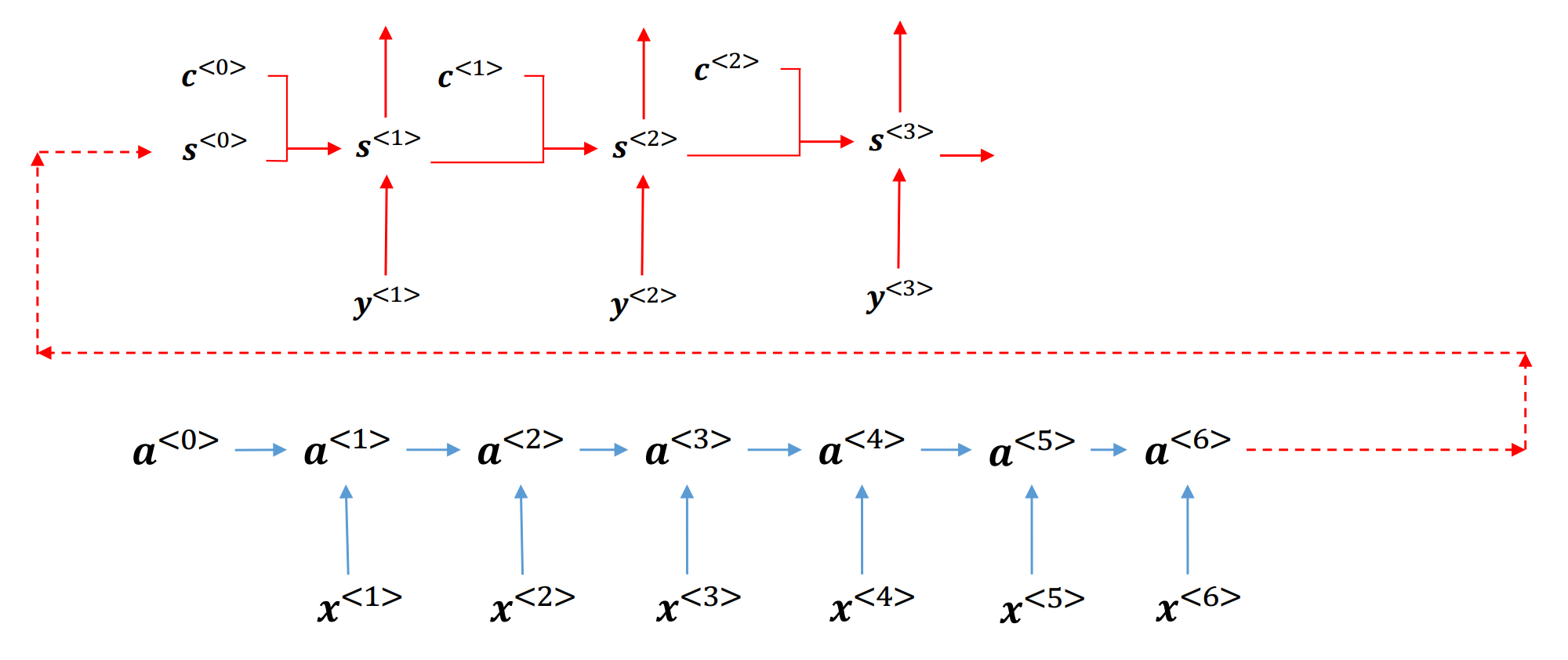
图 29 注意力机制的基本结构

\(\hspace{1.5em}\) 在上图中， \(a_t \in \mathcal{R}^{d_h}\) 是编码器的隐藏状态，\(a_t=s_0 \in \mathcal{R}^{d_h}\) 是编码器最后的隐藏状态，同时也是解码器的初始隐藏状态。与普通的seq2seq不同，在基于注意力机制的解码器其中，我们会多一个上下文变量 \(c_t \in \mathcal{R}^{d_h}\)。简单来说这个 \(c_t\) 是编码器中各个时刻隐藏状态的 加权平均。我们可以理解为，假设时刻 \(t\) 中编码器的输入很重要，那么其权重就会更大，反之则权重更小。那么我们应该怎么去衡量这个权重呢？假设我们考虑输入和输出是一对一的情况，也就是说，在每一个时刻 \(t\) 编码器的输入和解码器的输出是也应该是一一对应的。在解码器中，时刻 \(t\) 时我们会有一个 \(a_t\) 作为编码器的隐藏状态，同时有一个 \(s_t\) 作为解码器的隐藏状态，如果两个隐藏状态相似，那么这两个隐藏状态对应的信息也是相似的。以机器翻译为例，如果输入序列的第 \(t\) 个词是“猫”，那么输出序列的第 \(t\) 个词也应该是“cat”。因此，我们可以使用一个函数来衡量这两个隐藏状态的相似程度，这个函数就是注意力机制的核心。通过将 \(s_t\) 与输入序列（编码器隐藏状态）一一计算相似度，最后我们可以通过 softmax 函数来得到权重，然后使用这些权重对编码器隐藏状态进行加权求和得到上下文变量 \(c_t\)。下面我们给出注意力机制的计算公式：

\[\begin{split}e_{ij} &= score(s_i, a_j)\\ \omega_{ij} &= \frac{\exp(e_{ij})}{\sum_{k=1}^{T} \exp(e_{ik})} \\ c_i &= \sum_{j=1}^{T} \omega_{ij} a_j\end{split}\]

\(\hspace{1.5em}\) 上面我们提到了我们可以使用一个函数来衡量两个隐藏状态的相似程度，下面我们将介绍几种文献中常用的计算相似度的方法：

• Content-base attention: \(score(s_i, a_j) = cosine(s_i, a_j)\) ；

• Additive: \(score(s_i, a_j) = v_a^{\top} \tanh(W_a s_i + U_a a_j)\)；

• Location-Base: \(score(s_i, a_j) = softmax(W_a s_i)\)；

• General: \(score(s_i, a_j) = s_i^{\top} W_a a_j\)；

• Dot-Product: \(score(s_i, a_j) = s_i^{\top} a_j\)；

其中， \(v_a, W_a, U_a\) 是需要学习的参数。

\(\hspace{1.5em}\) 在上一小节中，我们介绍了在seq2seq架构中如何使用注意力机制来获取全局的信息。其基本思想是，通过对编码器的隐藏状态进行加权求和，得到一个上下文变量，然后将这个上下文变量与解码器的隐藏状态进行拼接，从而更好的捕捉序列中的信息。既然能通过注意力机制来获取整个序列的信息，那么我们是不是可以舍弃RNN中的循环结构呢？答案是肯定的。下面，我们将介绍自注意力机制（self-attention mechanism）以及位置编码（positional encoding）。

自注意力机制

\(\hspace{1.5em}\) 在循环神经网络中，序列之间的相关性是通过隐藏状态（在LSTM中还包括了单元状态）来进行传递的。假设输入序列为 \(x_1, x_2, \dots, x_T\)，我们的目标是在每一个时刻 \(t\) 获得当前输入的一个潜在表达形式 \(h_t\)。如果我们不使用循环结果，而是使用注意力机制来捕捉序列间的相关性，那么我们可以考虑使用如下方式：

\[\begin{split}e_{t,i} &= \text{score}(x_t, x_i) \\ \alpha_{t,i} &= \frac{\exp(e_{t,i})}{\sum_{k=1}^{n} \exp(e_{t,k})} \\ h_t &= \sum_{i=1}^{n} \alpha_{t,i} x_i\end{split}\]

\(\hspace{1.5em}\) 在自注意力机制中，我们是将 \(t\) 时刻的输入 \(x_t\) 与所有输入 \(x_i, i = 1, \dots, T\) 进行比较，然后通过 softmax 函数得到权重，最后以这些权重对输入进行加权得到上下文变量 \(h_t\)。这样的好处在于，我们可以同时考虑到所有的输入，而不是像RNN一样一个接一个的考虑。由上述公式我们可以发现，自注意力机制的计算方式与普通的注意力机制的计算方式是完全相同的。不过在自注意力中，是将 \(t\) 时刻的输入与所有输入进行比较；而在普通注意力机制中，将 \(t\) 时刻解码器的隐藏状态与所有编码器的隐藏状态进行比较。

位置编码

\(\hspace{1.5em}\) 在自注意力机制中，我们是对所有的输入进行比较，然后通过 softmax 函数得到权重。这种情况下，自注意力机制没办法考虑到输入的顺序信息。为了解决这个问题，我们可以引入位置编码（positional encoding）。位置编码是指，我们为每一个输入的位置添加一个特定的编码，这样就能保留输入的顺序信息。这个编码信息可以是预先设定（pre-specified），也可以作为参数进行学习。

\(\hspace{1.5em}\) 假设输入序列为 \(x_1, x_2, \dots, x_T \in \mathcal{R}^d\)，位置编码需要与输入的维度相同。例如，对于 \(x_i\) 第 \(2j\) 和第 \(2j + 1\) 上的元素，我们可以使用如下公式进行编码 ^{17 17}该位置编码可以理解为二进制的浮点数表示，具体参见 《动手学深度学习（中文版）》 第10章。：

\[\begin{split}PE_{(i, 2j)} &= \sin(i / 10000^{2j / d}) \\ PE_{(i, 2j + 1)} &= \cos(i / 10000^{2j / d})\end{split}\]

\(\hspace{1.5em}\) 最后通过将 \(x_i\) 与位置编码 \(PE_{i}\) 相加，我们就能得到一个新的输入向量，从而保留输入的顺序信息。

¹⁸推荐阅读 Attention is All You Need 以及观看视频 Transformer论文逐段精读【论文精读】。

Transformer ^{18 18}推荐阅读 Attention is All You Need 以及观看视频 Transformer论文逐段精读【论文精读】。

\(\hspace{1.5em}\) 在之前的章节中，我们介绍了RNN及其拓展模型LSTM和GRU。在实际应用中，这些模型取得了非常不错的结果。但是，循环神经网络（RNNs）存在的一个非常大的缺陷是，不能并行化。这是因为我们在计算 \(t\) 时刻隐藏状态时，必须要先计算出 \(h_{t-1}\)。以输入为一个句子为例，循环神经网络是一个词一个词处理。以人类阅读为例，这种方式的阅读效率是非常低的，这就导致这些模型在实际应用中会有一定局限性。除此之外，我们也提到过，针对于长序列，循环神经网络在实际应用时也会存在许多问题。下面，我们将介绍大语言模型的基础：Transformer。为了更好的理解Transformer，我们首先给出Transformer的基本结构，然后分别介绍每个部分的计算方式，最后，以 pytorch 库中的 Transformer 为例来说明Transformer是如何实现的。

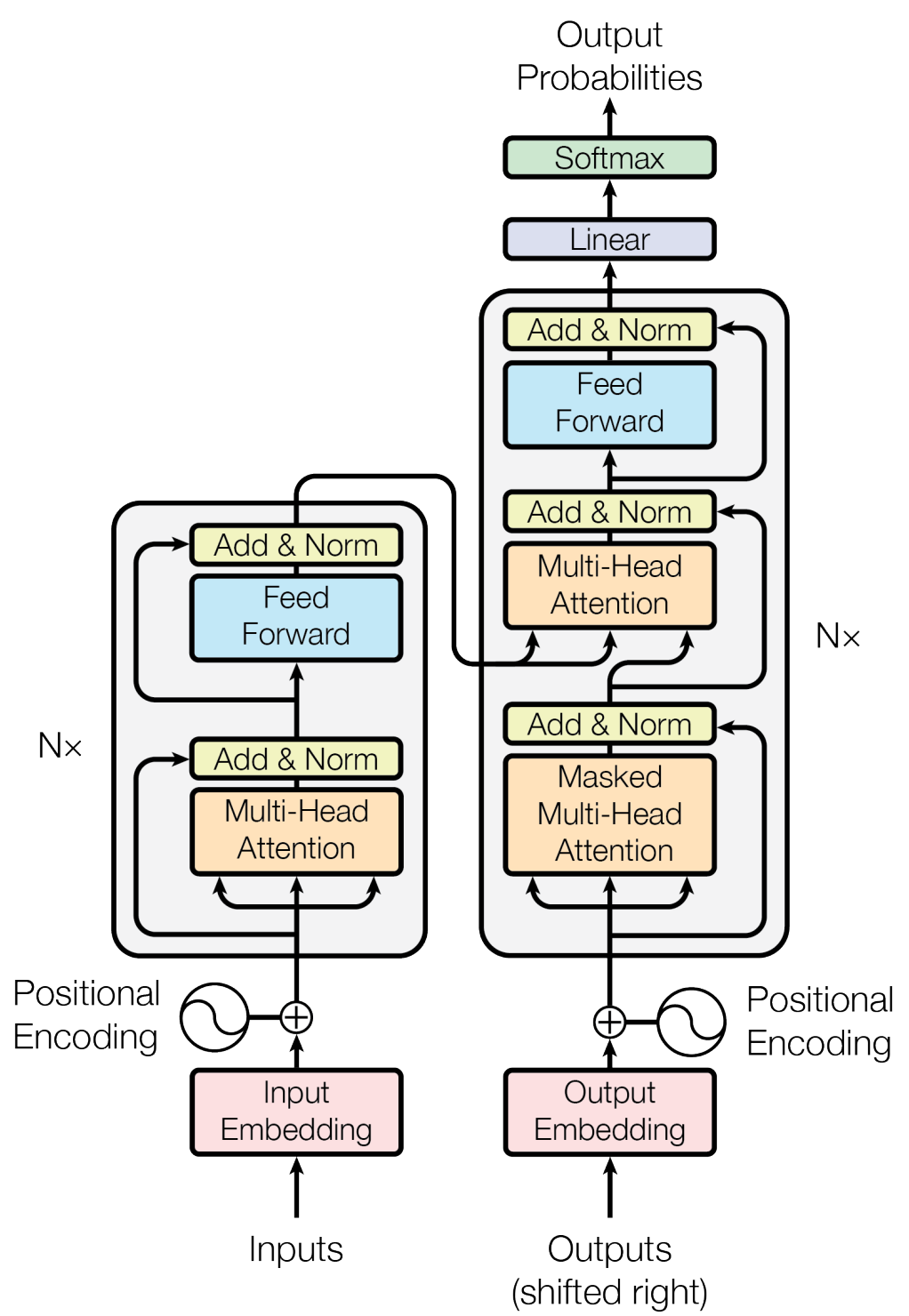
图 30 Transformer模型的基本结构

\(\hspace{1.5em}\) 从上图我们可以发现，Transformer使用了经典的seq2seq架构，其中编码器和解码器旁边的 Nx 表示由 N 个完全相同的块（block）堆叠（stack）在一起。和之前的模型相比，Transformer多了一些额外的操作，例如（带掩码的，Masked）多头自注意力机制（Multi-Head-Attention，MHA），层次归一化（Layer Normalization，Add&Norm）等。忽略这部分，Transformer就和普通的seq2seq架构一样：输入是一个文本序列，输出是一个下一个词元概率分布。下面，我们先从多头注意力机制开始介绍Transformer的组成结构。

多头自注意力机制（Multi-Head-Attention，MHA）

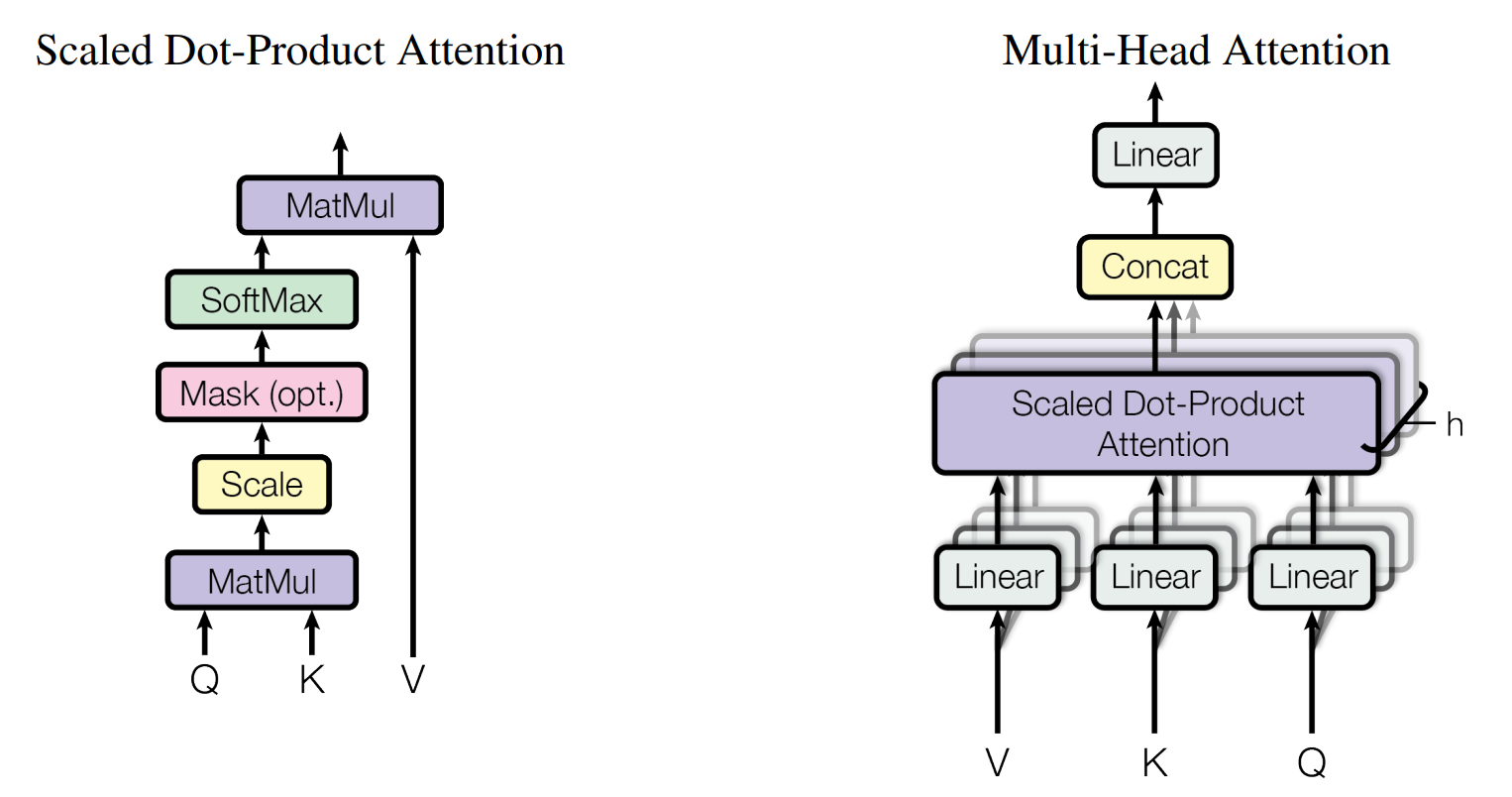
图 31 注意力机制（左）和多头注意力机制（右）示意图。

\(\hspace{1.5em}\) 上图给出了Transformer中多头自注意力机制的示意图。其中左边部分与之前介绍过的自注意力机制相同，核心思想也是对输入变量进行加权求和；而右边的多头（Multi-Head）可以与CNN中的通道（Channel）做类比，用于学习不同类型的相关性。假设我们的序列为 \(X = (x_1, \dots, x_T)^{\top} \in \mathcal{R}^{T \times d}\)，为了对自注意力的计算进行矩阵操作，这里使用了 查询（Query，Q），键（Key，K） 以及 值（Value，V） 来进行计算，我们首先给出三个矩阵的计算公式：

\[Q = X W_Q, K = X W_K, V = X W_V,\]

其中 \(W_Q \in \mathcal{R}^{d \times d_k}, W_K \in \mathcal{R}^{d \times d_k}, W_V \in \mathcal{R}^{d \times d_v}\) 是需要学习的参数，\(d_k\) 是 Q 和 K 的维度，\(d_v\) 是 V 的维度。然后我们可以通过如下公式计算注意力分数（基于 Dot-Product）：

\[\text{Attention}(Q, K, V) = \text{softmax}(\frac{Q K^{\top}}{\sqrt{d}}) V \in \mathcal{R}^{n \times d_v}.\]

\(\hspace{1.5em}\) 在注意力机制中：

1. Query ：代表了我们正在询问的信息或我们关心的上下文。在自注意力机制中，每个序列元素都有一个对应的查询，它试图从其他部分找到相关信息。

2. Key ：这是可以查询的条目或“索引”。在自注意力机制中，每个序列元素都有一个对应的键。

3. Value ：对于每一个“键”，都有一个与之关联的“值”，它代表实际的信息内容。当查询匹配到一个特定的键时，其对应的值就会被选中并返回。

\(\hspace{1.5em}\) 这种思路与数据库查询非常相似，可以将 Query 看作是搜索查询，Key 看作是数据库索引，而 Value 则是实际的数据库条目。以自注意力机制为例，我们需要序列中每个时刻的值 \(x_t\) （Query）与所有时刻的值 \(x_1, x_2, \dots, x_T\) （Key）进行比较，然后通过 softmax 函数得到权重，最后将这些权重与所有时刻的值 \(x_1, x_2, \dots, x_T\) （Value）相乘，得到最终的输出。放到普通的注意力机制中，Query 就是解码器中的隐藏状态，Value 就是编码器中的隐藏状态，Key 就是编码器中的隐藏状态。

\(\hspace{1.5em}\) 多头自注意力中的多头，与CNN中的 多通道 类似，通过不同的 \(W_Q, W_V, W_k\) （类似于CNN中的 kernel ）来学习不同类型的相关性。在实际应用中，我们可以设置多个头，然后将这些头的输出进行拼接，最后通过一个线性变换得到最终的输出。下面我们给出多头自注意力的计算公式：

\[\begin{split}\text{MultiHead}(Q, K, V) &= \text{Concat}(\text{head}_1, \dots, \text{head}_h) W^O \\ \text{head}_i &= \text{Attention}(Q_i, K_i, V_i),\end{split}\]

其中 \(Q_i = X W_i^Q, K_i = X W_i^K, V_i = X W_i^V\)， \(W_i^Q \in \mathcal{R}^{d \times d_k}, W_i^K \in \mathcal{R}^{d \times d_k}, W_i^V \in \mathcal{R}^{d \times d_v}\) 是需要学习的参数， \(W^O \in \mathcal{R}^{h*d_v \times d}\) 是需要学习的参数， \(h\) 是头的个数。在Transformer中，\(h = 8\)，\(d = 512\)，\(d_k = d_v = 64\)。

掩码操作（masked MHA）

\(\hspace{1.5em}\) 上一小节中，我们介绍了多头自注意力机制。但是我们发现，在Transformer的解码器中，有一个特殊的结构叫做带掩码的自注意力机制，下面我们先介绍为什么需要带掩码的自注意力机制，然后介绍掩码操作的计算方式。

\(\hspace{1.5em}\) RNN在进行预测 ^{19 19}需要注意的是，RNN中的预测是自回归的，也就是说，我们在预测时，总是需要先拿到前一时刻的预测，然后再预测下一个时刻的输出。在 训练阶段，我们是将真实的标签作为输入，然后预测下一个时刻的输出；而在 预测阶段，我们是将前一时刻的预测作为输入，然后预测下一个时刻的输出。Transformer中同样是如此。 时，总是需要先拿到前一时刻的预测 \(\hat y_{t-1}\)，将 \(\hat y_{t-1}\) 作为输入，然后再预测下一个时刻的输出 \(\hat y_t\) （自回归）。但是在Transformer中，模型训练时我们是一次性拿到整个序列的输入，然后一次性输出整个序列的输出。这就导致了一个问题，如果我们在预测时，拿到了后面的信息，那么这个信息就会影响到前面的预测 ^{20 20}因为Transformer在计算注意力时是对整个句子中的每个词进行加权求和，因此在预测时，如果拿到了后面的信息，那么这个信息就会影响到前面的预测。。为了解决这个问题，我们需要将后面的信息隐藏起来。掩码操作的思想是，我们在预测时，只能看到当前时刻之前的信息，而不能看到当前时刻之后的信息。这样就能保证我们的预测不会受到未来信息的影响。

\(\hspace{1.5em}\) 在Transformer中，一共有三种掩码：

1. Padding Mask：之前我们提到，文本序列的长度通常是不一样的，为了保证输入序列的长度一致（这样才能使用定长的 tensor 来计算）。对于较长的序列，通常会对序列进行截断；而对于较短的序列，通常会在序列后面加上一些特殊的符号。在Transformer中，通常使用 <PAD> 词元作为填充符号，这样就会导致一些无效的信息。为了让模型能够忽略这些无效信息，我们需要引入填充掩码，将填充的位置的权重设置为0，这样就能保证填充的位置不会对模型的训练产生影响；

2. Attention Mask：上面我们提到，为了保证在预测时，只能看到当前时刻之前的信息，在每个时刻我们要保证当前时刻之后的信息不能被看到。在Transformer中，我们可以通过将当前时刻之后的信息设置为负无穷，然后通过 softmax 函数得到的权重就会接近于0，这样就能保证在预测时，只能看到当前时刻之前的信息；

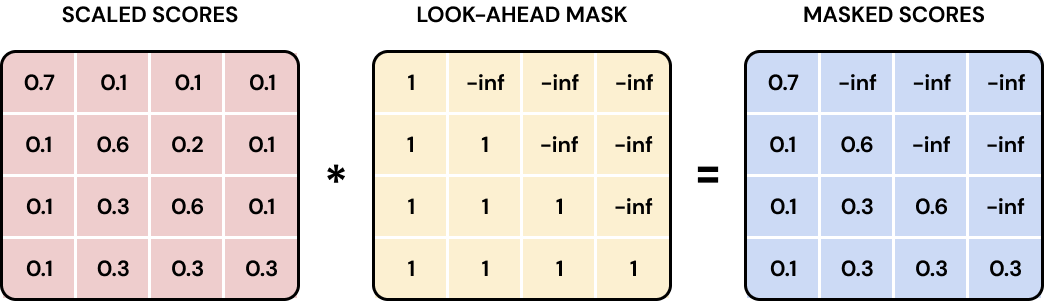
图 32 Attention Mask的示意图。（图片来源：Transformers: The Nuts and Bolts ）

3. Sequence Mask：用于隐藏输入序列的某些部分。例如，在双向模型（BERT）中，我们可能希望根据特定标准忽略序列的某些部分。

Layer Normalization

\(\hspace{1.5em}\) 在之前的章节中，我们介绍了通过批量归一化（Batch Normalization）来解决内部变量偏移（internal covariate shift）的问题。故名思义，批量归一化是在 Batch 的维度上做归一化。在序列数据中，输入的维度通常是 [batch_size, seq_len, embedding_dim]，批量归一化是指对于每一个 embedding_dim，计算均值和方差，然后对整个 batch 进行归一化。但是在RNN中，由于序列的长度是不一样的，因此我们无法在 Batch 的维度上做归一化。为了解决这个问题，我们可以使用层次归一化（Layer Normalization）。层次归一化是指，对每一个 batch 和 seq_len，分别做归一化 。下面我们给出层次归一化的计算公式以及两种归一化方式的对比：

\[\text{LayerNorm}(x) = \gamma \odot \frac{x - \mu}{\sqrt{\sigma^2 + \epsilon}} + \beta,\]

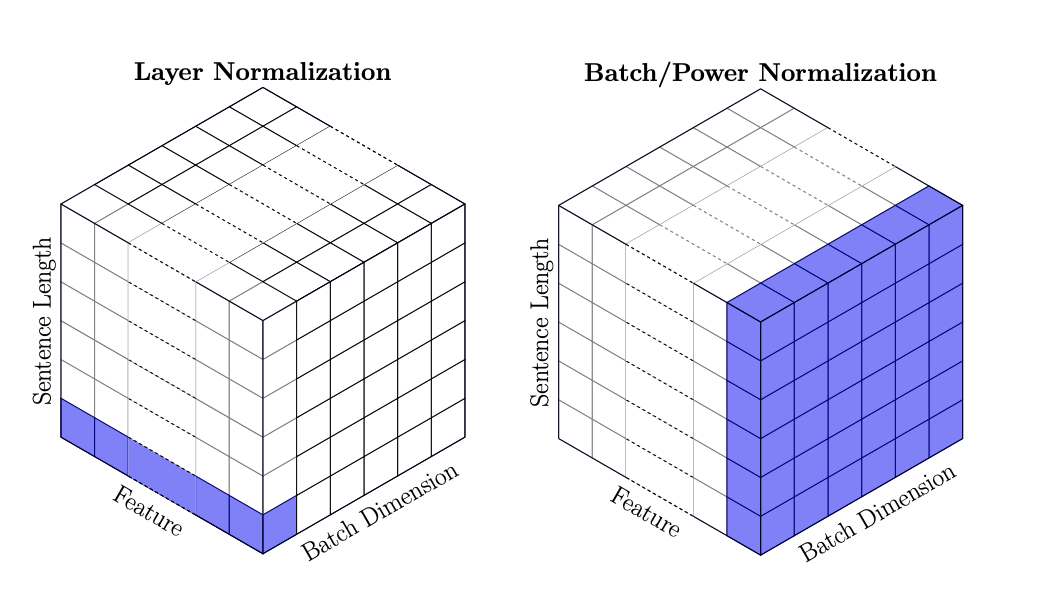
图 33 层次归一化和批量归一化的对比。（图片来源：Shen et al. (2020) ）

\(\hspace{1.5em}\) 下面，我们以 pytorch 中的 LayerNorm 和 BatchNorm1d 为例来介绍这两种归一化方式的区别：

import torch
import torch.nn as nn

# 假设输入是文本序列，那么输入的维度为 [batch_size, seq_len, embedding_dim]
# 即：batch_size 个句子，每个句子有 seq_len 个词，每个词用 embedding_dim 维的向量表示
batch_size, seq_len, embedding_dim = 2, 2, 3

# 创建一个张量，x = [batch_size, seq_len, embedding_dim]
w = [[[1, 2, 4], [2, 3, 4]], [[3, 4, 4], [4, 4, 4]]]
w = torch.tensor(w, dtype=torch.float32)

# 定义层次归一化
layer_norm = nn.LayerNorm(embedding_dim)
layer_norm_output = layer_norm(w)

# 定义批量归一化
batch_norm = nn.BatchNorm1d(embedding_dim)
# BatchNorm1d 期望输入的形状为 (batch_size, embedding_dim, seq_len)
# 请参考 nn.BatchNorm1d 的官方文档
batch_norm_output = batch_norm(w.permute(0, 2, 1)).permute(0, 2, 1)

# 打印张量和归一化后的输出
print('原始向量：')
print(w)
print('层次归一化结果：')
print(layer_norm_output.data)
print('批量归一化结果：')
print(batch_norm_output.data)

\(\hspace{1.5em}\) 上述代码会产生如下结果：

原始向量：
tensor([[[1., 2., 4.],
         [2., 3., 4.]],

      [[3., 4., 4.],
         [4., 4., 4.]]])
层次归一化结果：
tensor([[[-1.0690, -0.2673,  1.3363],
         [-1.2247,  0.0000,  1.2247]],

      [[-1.4142,  0.7071,  0.7071],
         [ 0.0000,  0.0000,  0.0000]]])
批量归一化结果：
tensor([[[-1.3416, -1.5075,  0.0000],
         [-0.4472, -0.3015,  0.0000]],

      [[ 0.4472,  0.9045,  0.0000],
         [ 1.3416,  0.9045,  0.0000]]])

\(\hspace{1.5em}\) 从上面的结果我们可以看到，层次归一化是在每个词的所有特征上做归一化，例如 x[2, 1] = [4, 4, 4] （第3个句子，第2个词），层次归一化后的结果是 [0, 0, 0]；而批量归一化是在每个特征的所有样本上做归一化，例如 x[:, :, 2] = [4, 4, 4, 4] （所有句子中，最后一个词的最后一个 feature），批量归一化后的结果是 [0, 0, 0, 0]。

数据流（dataflow）

\(\hspace{1.5em}\) 在了解了Transformer的基本结构之后，下面我们按照模型的工作流程来介绍Transformer的计算方式 ^{21 21}针对Transformer的实现，可以参考 The Annotated Transformer 。针对Transformer数据流的可视化，可以参考 Transformer Explainer。。我们首先打印 pytorch 中 transformer 的结构，然后按照源码的顺序来介绍Transformer的计算方式。

from torch.nn import Transformer

# 定义一个Transformer模型
model = Transformer(d_model=512, nhead=8, num_encoder_layers=6, num_decoder_layers=6, dim_feedforward=2048, batch_first=True)

# 打印模型结构
print(model)

\(\hspace{1.5em}\) 上述代码的运行结果为：

Transformer(
   (encoder): TransformerEncoder(
      (layers): ModuleList(
         (0-5): 6 x TransformerEncoderLayer(
         (self_attn): MultiheadAttention(
            (out_proj): NonDynamicallyQuantizableLinear(in_features=512, out_features=512, bias=True)
         )
         (linear1): Linear(in_features=512, out_features=2048, bias=True)
         (dropout): Dropout(p=0.1, inplace=False)
         (linear2): Linear(in_features=2048, out_features=512, bias=True)
         (norm1): LayerNorm((512,), eps=1e-05, elementwise_affine=True)
         (norm2): LayerNorm((512,), eps=1e-05, elementwise_affine=True)
         (dropout1): Dropout(p=0.1, inplace=False)
         (dropout2): Dropout(p=0.1, inplace=False)
         )
      )
      (norm): LayerNorm((512,), eps=1e-05, elementwise_affine=True)
   )
   (decoder): TransformerDecoder(
      (layers): ModuleList(
         (0-5): 6 x TransformerDecoderLayer(
         (self_attn): MultiheadAttention(
            (out_proj): NonDynamicallyQuantizableLinear(in_features=512, out_features=512, bias=True)
         )
         (multihead_attn): MultiheadAttention(
            (out_proj): NonDynamicallyQuantizableLinear(in_features=512, out_features=512, bias=True)
         )
         (linear1): Linear(in_features=512, out_features=2048, bias=True)
         (dropout): Dropout(p=0.1, inplace=False)
         (linear2): Linear(in_features=2048, out_features=512, bias=True)
         (norm1): LayerNorm((512,), eps=1e-05, elementwise_affine=True)
         (norm2): LayerNorm((512,), eps=1e-05, elementwise_affine=True)
         (norm3): LayerNorm((512,), eps=1e-05, elementwise_affine=True)
         (dropout1): Dropout(p=0.1, inplace=False)
         (dropout2): Dropout(p=0.1, inplace=False)
         (dropout3): Dropout(p=0.1, inplace=False)
         )
      )
      (norm): LayerNorm((512,), eps=1e-05, elementwise_affine=True)
   )
)

其中 self_attn 表示编码器和解码器中的 Multi-head Attention； multihead_attn 表示解码器中的 Masked Multi-head Attention；linear、layer_norm、dropout 分别表示全连接层、层次归一化和 Dropout 层。下面以英文翻译中文为例来解释Transformer中的数据流。假设输入是一段英文文本，输出是翻译的中文文本（文本序列长度不同）。令 \(w_1, w_2, \dots, w_n\) 为原始输入文本（Transformer模型的基本结构 中的 Inputs），语料中一共有 \(\mathcal{V}\) 个词，Transformer中的数据流（模型训练阶段）可以表示如下：

• 编码器：

  ²²在实际应用中，还需要对原始序列进行截断或者填充，同时会加上一些特殊词元（例如 <bos>, <eos> 等）。通常来说，这一个操作可以通过模型自带的 tokenizer 实现。

  1. 词元化：首先，我们需要将输入文本转换为词元（token）的形式，然后利用词表（vocabulary）将需入序列转换为一个长度相同的 id 序列 \(v_1, v_2, \dots, v_n\) ^{22 22}在实际应用中，还需要对原始序列进行截断或者填充，同时会加上一些特殊词元（例如 <bos>, <eos> 等）。通常来说，这一个操作可以通过模型自带的 tokenizer 实现。。

  ²³请参考 nn.Embedding 的官方文档。其本质是将标量（id）映射为向量（embedding）。这里的 embedding 可以看作是每一个词元的原始词嵌入，并没有利用上下文信息。

  2. 词嵌入：拿到 id 序列之后，我们需要将这些 id 转换为对应的词向量。这个操作可以通过 Embedding 层来实现，假设词向量的维度为 \(d = 512\)，那么我们可以用 nn.Embedding() ^{23 23}请参考 nn.Embedding 的官方文档。其本质是将标量（id）映射为向量（embedding）。这里的 embedding 可以看作是每一个词元的原始词嵌入，并没有利用上下文信息。 来实现。最后，我们拿到了原始的词嵌入向量 \(x_1, x_2, \dots, x_n \in \mathcal{R}^{d}\)，这也就是 Transformer模型的基本结构 中的 Input Embedding。为了保证 embedding 和 positional encoding 相比数值上不会太小，Transformer在会将 embedding 乘以一个系数 \(\sqrt{d}\)。

  3. 添加位置编码：对于词嵌入向量，我们需要添加位置编码。计算每个位置的位置编码后，会直接将位置编码与词嵌入向量相加，得到新的输入向量。我们用 \(x_1, x_2, \dots, x_n \in \mathcal{R}^{d}\) 来表示添加位置编码后的输入向量。

  ²⁴在多头自注意力机制中，我们将输入向量的维度 \(d\) 分为 \(h\) 个头，每个头的维度为 \(d_v = d_k = d / h\)。最后拼接在一起的向量维度仍然为 \(d\)。

  4. 多头自注意力机制：对于添加位置编码后的输入向量，我们需要通过多头自注意力机制来获取全局的信息。由于是自注意力机制，因此我们对每个向量乘上一个矩阵 \(W_Q, W_K, W_V \in \mathcal{R}^{d \times d / h}\) ^{24 24}在多头自注意力机制中，我们将输入向量的维度 \(d\) 分为 \(h\) 个头，每个头的维度为 \(d_v = d_k = d / h\)。最后拼接在一起的向量维度仍然为 \(d\)。 得到每个向量对应的 \(Q, K, V \in \mathcal{R}^{d / h}\) 值，最后拿到加权后的输出向量 \(z_{h, 1}, z_{h, 2}, \dots, z_{h_n} \in \mathcal{R}^{d / h}\)。通过将每个头对应位置的向量拼接在一起，我们就得到了最终的输出向量 \(z_1, z_2, \dots, z_n \in \mathcal{R}^{d}\)。

  5. Add&Norm：在这一步，我们需要将多头自注意力机制的输出向量与输入向量相加（与 Resnet 相似），然后再进行层次归一化，最后输出 \(x_1, x_2, \dots, x_n \in \mathcal{R}^{d}\)。

  6. 逐位置的MLP：在这一步，我们需要对 Add&Norm 的输出向量进行全连接操作，先将维度增加到 \(d_{ff} = 2048\)，然后再将维度降回到 \(d = 512\)。计算公式为:math:MLP(x) = ReLU(xW_1 + b_1)W_2 + b2。这一步对应 Transformer模型的基本结构 中的 Feed Forward，在代码中包括了 linear1、linear2。最后得到 \(x_1, x_2, \dots, x_n \in \mathcal{R}^{d}\)。

  7. Add&Norm：与步骤 5 相同。

  8. 重复步骤 4-7，N=6 （编码器层数）次。注意在这个过程中，每个块的输入和输出维度都是不变的，所以最后我们拿到的还是 \(x_1, x_2, \dots, x_n \in \mathcal{R}^{d}\)。

• 解码器：

  1. 与编码器中的步骤1-3相同，我们将目标序列（中文）转换为了词嵌入向量 \(y_1, y_2, \dots, y_n \in \mathcal{R}^{d}\)。值得注意的是，Transformer的编码器和解码器使用了同一个词嵌入矩阵。

  2. 带掩码的自注意力机制：与编码器中步骤 4 类似，只是在计算注意力得分时，我们需要引入掩码操作。最后我们同样拿到了 \(y_1, y_2, \dots, y_n \in \mathcal{R}^{d}\)。

  3. Add&Norm：与编码器中的步骤 5 相同。

  4. 注意力机制：在这一步，我们将编码器中的输出作为 Key 和 Value，将带掩码的自注意力机制的输出作为 Query，然后通过多头自注意力机制得到最终的输出。

  5. Add&Norm：与编码器中的步骤 5 相同。

  6. 逐位置的MLP：与编码器中的步骤 6 相同。

  7. Add&Norm：与编码器中的步骤 5 相同。

  8. 重复步骤 2-7，N=6 （解码器层数）次。最后拿到 \(y_1, y_2, \dots, y_n \in \mathcal{R}^{d}\)。

  9. token to id：这一步骤与编码器中的步骤 2 相反，是通过 Embedding 层将词嵌入向量转换为 id 序列，可以通过线性变换实现。

  10. Softmax：通过 Softmax 函数得到最终的输出概率分布。

Transformer中的Dropout

\(\hspace{1.5em}\) 在Transformer中，Dropout 出现在三个地方。第一个是多头自注意力机制当中，对 Attenion(Q, V, K) 执行 dropout 操作，对应代码中的 dropout；第二个是加上位置编码后的 embedding 之后，即编码器中的步骤 3 （解码器的步骤 1）之后；第三个个是层归一化之前，对应代码中的 dropout1，dropout2，dropout3。Transformer的层归一化通常是在 Add 之后，因此可以表示为 \(\text{LayerNorm}(x + \text{Dropout}(f(x)))\)，其中 \(f(x)\) 表示 Multi-head Attention 或 Feed Forward 的输出。

²⁵推荐阅读 BERT原文 以及观看视频 BERT 论文逐段精读【论文精读】。

BERT ^{25 25}推荐阅读 BERT原文 以及观看视频 BERT 论文逐段精读【论文精读】。

\(\hspace{1.5em}\) 在探索自然语言理解的过程中，BERT（ B idirectional E ncoder R epresentations from T ransformers）的出现是又一个重要的里程碑。BERT从大量无标记数据集中训练得到的语言的向量表示（text representation，可以理解为embedding），可以显著提高各项自然语言处理任务的准确率。与传统的单向模型不同，BERT通过双向训练，使模型能够从前后文中更精确地理解词语的含义，从而在机器翻译、情感分析、文本摘要等任务上表现出色。

图 34 BERT的结构示意图。（图片来源： 维基百科 ）

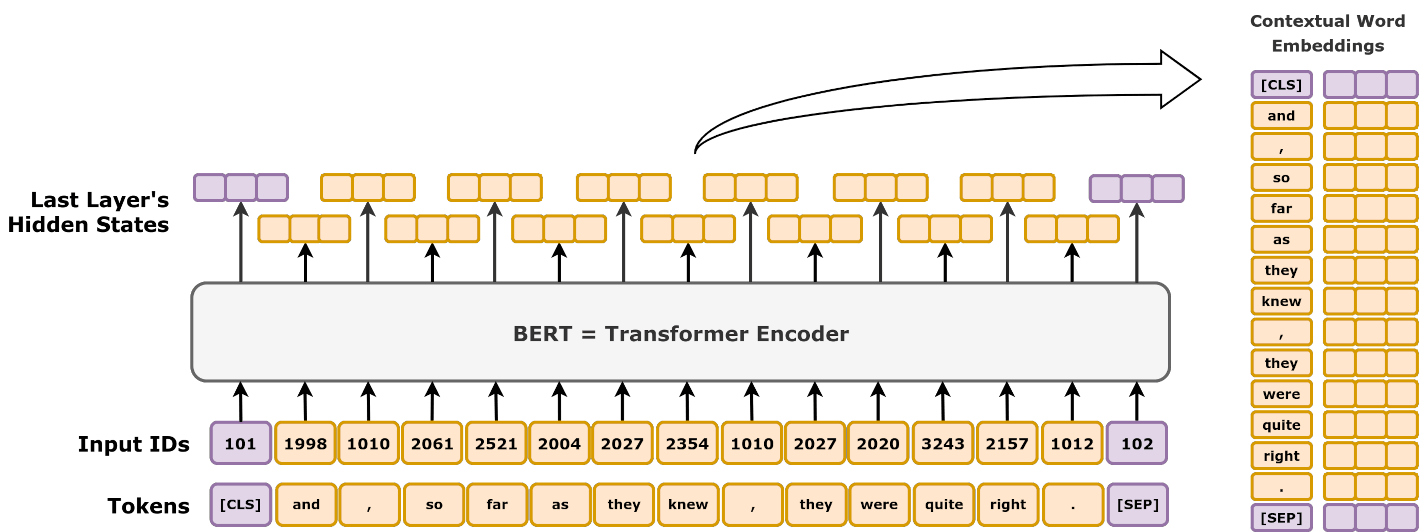
\(\hspace{1.5em}\) 从BERT的名字来看，我们可以分为两部分：双向（Bidirectional）的Transformer编码器（Encoder Representations from Transformers）。双向是指BERT在训练时，可以同时看到前后文，这样就能更好地理解词语的含义。与之相对应的，在Transformer的解码器中，因为使用了带掩码的自注意力机制，因此只能看到历史信息。使用双向信息的好处在于，能够更好的提取词语的意思。例如针对句子：“今天天气真___，我们可以出去徒步了！”。如果我们只看到“今天天气真”这部分，我们是无法判断下一个词想要表达的意思是“好”还是“坏”。但是如果我们能够看到空格后面的内容，我们就能判断空格部分应该是与“好”相关的词，这就是利用双向信息带来的好处。

\(\hspace{1.5em}\) 从模型结构来看，BERT与Transformer的编码器结构非常相似，只是对一些模型超参数进行了修改。针对不同的参数量，BERT一共有两个版本： BERT-base （110M参数）和``BERT-large`` （340M参数）：

1. 编码器层数：BERT-base 有12层，BERT-large 有24层（Transformer 中是6）；

2. 模型维度：BERT-base 的隐藏层维度为768，BERT-large 的隐藏层维度为1024（Transformer 中是512）；

3. 多头注意力中的头数：BERT-base 有12个头，BERT-large 有16个头（Transformer 中是8个头）；

\(\hspace{1.5em}\) 除此之外，BERT对输入的词嵌入做了如下修改：

1. 使用 WordPiece 词表，将词表中的词分割为子词。例如在英文中，单词 playing 可以被分割为 play 和 ##ing。这样做的好处是可以减少词表的大小，同时可以更好地处理未知词；

2. BERT在输入词嵌入时，引入了三个特殊的词元：[CLS]、[SEP] 和 [MASK]。其中 [CLS] 用于分类任务的输出，[SEP] 用于分隔两个句子，[MASK] 用于预训练任务。对于输入来说，最终输入的 Embedding 是 token embedding （通过embedding矩阵映射得到的值）、 segment embedding （第一个句子和第二个句子有不同的embedding） 和 position embedding （位置编码）之和：

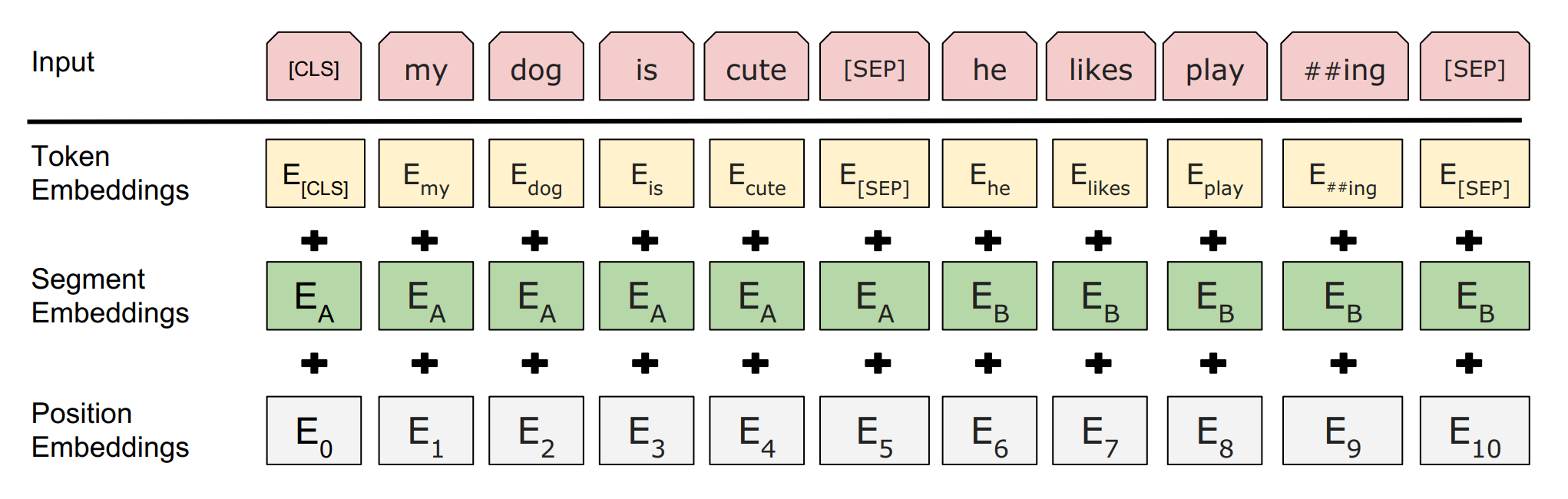
图 35 BERT的输入词嵌入示意图。

\(\hspace{1.5em}\) 从模型上看，BERT对于Transformer的改动比较少，真正让BERT能够取得成功的原因在于其可以通过大量无标记数据进行预训练，然后再通过少量标记数据进行微调。在预训练阶段，BERT通过两个任务来训练模型：Masked Language Model（MLM）和 Next Sentence Prediction（NSP）。在本节中，我们首先会介绍预训练和微调，以及这样做带来的好处；然后我们会介绍BERT是如何通过预训练来提取文本特征的；最后我们会用一个例子介绍如何使用BERT进行情感分析。

\(\hspace{1.5em}\) 在训练深度学习模型时，我们通常从（随机）初始化模型参数开始，然后通过梯度下降或其变体算法逐步更新这些参数。在模型参数较少且数据量有限的情况下，这种直接训练的方式通常能够取得良好的效果。随着模型参数数量的增加，模型的表达能力往往会提升，因此构建大规模模型（即包含更多参数）成为一种常见的选择。然而，参数数量的增加也带来了新的挑战：更复杂的模型需要更大的数据集来避免过拟合。特别是在自然语言处理领域，由于大规模标注数据的稀缺，直接训练大模型在实践中难以实现。为此，“预训练”（Pre-training）和“微调”（Fine-tuning）两步训练方法逐渐成为主流方式。

\(\hspace{1.5em}\) 在预训练阶段，我们使用大量无标记数据来训练模型，让模型能够学习语言的基本结构和潜在规律，从而积累丰富的通用知识。这为模型在后续任务中的表现打下了坚实的基础。随后，在微调阶段，我们将少量标记数据用于进一步调整模型，使其能够适应特定的任务需求。通过这种方法，模型可以将预训练中获得的通用知识迁移到具体任务上，在数据有限的条件下依然取得良好表现。这种分步训练法不仅缓解了数据稀缺的问题，还显著提高了模型的泛化能力和训练效率。

\(\hspace{1.5em}\) 从直观上理解，预训练阶段就像是学徒学习手艺的入门阶段。学徒会通过观察和实践，掌握一些基础的工具使用和操作方法，这是为后续专攻某一方向打下的基础。而微调阶段则类似于学徒在进入某个具体领域后，接受有针对性的培训。例如，原本学徒掌握了木工的基本技能，但在学习制作家具时，需要专注于特定技巧，比如精细雕刻或拼接。类似地，预训练帮助模型掌握通用的语言知识，而微调则让模型根据具体任务的需求进行专门的调整。

\(\hspace{1.5em}\) 在实际应用中，我们会将预训练得到的权重作为模型的初始值（类似于贝叶斯分析中的先验分布，prior distribution），然后在模型中添加一个 随机初始化 的任务特定层（task-specific head），用于处理具体任务。接下来，我们使用与该任务（down-stream task）相关的数据对整个模型进行微调（继续训练模型）。这样做的好处在于，预训练模型已经具备了大量的通用知识，因此在微调阶段，模型不仅可以更快地收敛，还能够更好地适应特定任务的需求，从而显著提高其在实际应用中的表现。

\(\hspace{1.5em}\) 通常来说，预训练对于数据量和计算资源要求较高，因此很多研究者会选择直接使用已经预训练好的模型，然后在自己的数据集上进行微调。这种方法不仅可以节省大量的时间和资源，还能够获得更好的效果。在本节的后续内容中，我们将介绍如何使用预训练的BERT模型进行情感分析任务。

BERT中的预训练任务

\(\hspace{1.5em}\) BERT模型的预训练任务是其创新的核心之一，为它在各种自然语言处理任务上取得的成功奠定了基础。在设计BERT时，BERT作者采用了两种预训练任务，即“掩码语言模型”（Masked Language Model, MLM）和“下一句预测”（Next Sentence Prediction, NSP）。这两种任务旨在帮助模型学习丰富的语言信息、句法结构、上下文依赖和句子间关系，使得模型在微调阶段能够有效适应多种语言理解任务。下面我们分别对这两个预训练任务进行详细介绍。

• 掩码语言模型（Masked Language Model, MLM）

\(\hspace{1.5em}\) 传统的语言模型通常是单向的，比如从左到右生成一个句子中的词语。然而，BERT的设计初衷是基于上下文理解句子中的所有词语。为此，BERT采用了“掩码语言模型”作为预训练任务，这是一种基于上下文的词预测方法。

\(\hspace{1.5em}\) 在MLM任务中，模型输入的句子中会随机选择一些词语并将其掩盖起来（即替换为特殊的 [MASK] 标记），然后要求模型基于句子的剩余部分来预测被掩盖的词语。例如，句子“我喜欢学习这门课”可能被掩盖为“我喜欢 [MASK] 这门课”，模型的任务是预测出被掩盖的词是“学习”。这种方式让模型在训练过程中学习到每个词语在不同上下文中的含义。与传统的单向语言模型不同，MLM能够让模型同时从左到右和从右到左的双向上下文中获得信息，从而增强模型的理解力。

\(\hspace{1.5em}\) MLM的具体操作过程包括两个步骤：

1. 随机掩盖词语：在句子中随机选择15%的词语来进行掩盖。被选中的词语会有80%的概率被替换为 [MASK] ，10%的概率替换为随机的另一个词语，剩下的10%概率保持不变。这样做是为了让模型更灵活地应对不同的情况，增强模型对词汇的泛化能力。

2. 预测掩盖词语：模型需要基于上下文信息，准确地预测出被掩盖的词语是什么。这要求模型不仅能识别单词的语义，还能理解其在句子中的具体含义和作用。

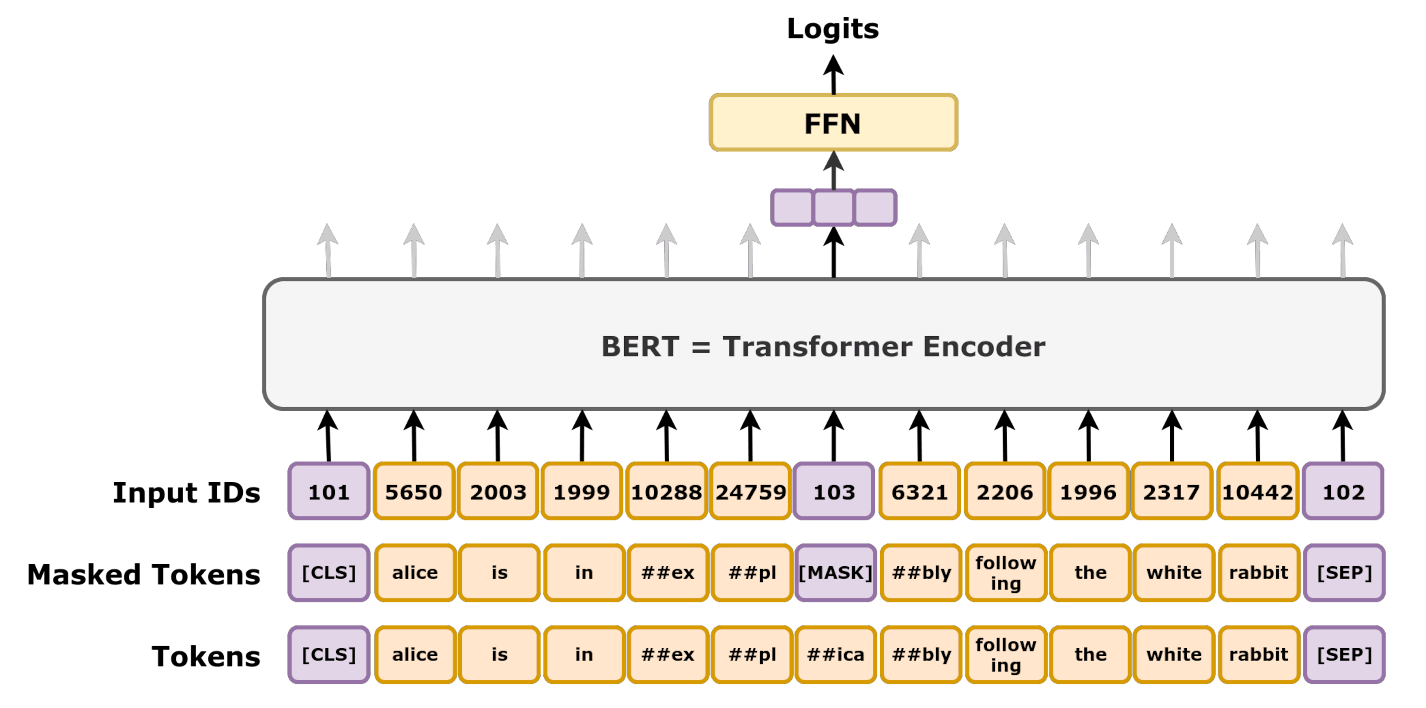
图 36 MLM示意图

\(\hspace{1.5em}\) MLM任务的设计使得BERT在训练中能够有效学习到语言的深层次特征，这为之后的微调任务提供了通用的语言表示能力。

• 下一句预测（Next Sentence Prediction, NSP）

\(\hspace{1.5em}\) 为了增强模型对句子间关系的理解，BERT还引入了“下一句预测”任务。这个任务的目标是帮助模型理解句子之间的逻辑关系，如连贯性和因果性，这对于一些需要句子理解的任务（例如自然语言推理、问答系统）尤为重要。

\(\hspace{1.5em}\) 在NSP任务中，BERT会从训练语料中随机选取句子对，句子对中的两个句子可能是实际连续的（即B句是A句的下一句），也可能是随机拼接的（即B句与A句没有实际联系）。模型的任务是判断给定的两个句子是否在原文本中是连续的。具体来说：

1. 构造句子对：模型随机选取50%的句子对是连续的句子对，剩下的50%为不连续的句子对。对于连续的句子对，句子B确实是句子A的下一句；而对于不连续的句子对，句子B则是从语料库中随机抽取的。

2. 模型输入格式：为了区分两个句子，BERT在输入中添加了特殊标记 [CLS] 和 [SEP]。 [CLS] 作为句子对的起始标记，用于最终的句子对分类输出；而 [SEP] 用于分隔句子A和句子B。输入格式通常为：[CLS] 句子A [SEP] 句子B [SEP]。

3. 预测句子关系：模型基于输入的句子对，通过 [CLS] 位置的输出预测这两个句子是否是连续的（本质上是二分类问题）。该任务在模型中增加了对句间关系的理解，使得BERT在需要跨句子信息的任务中表现更优异。

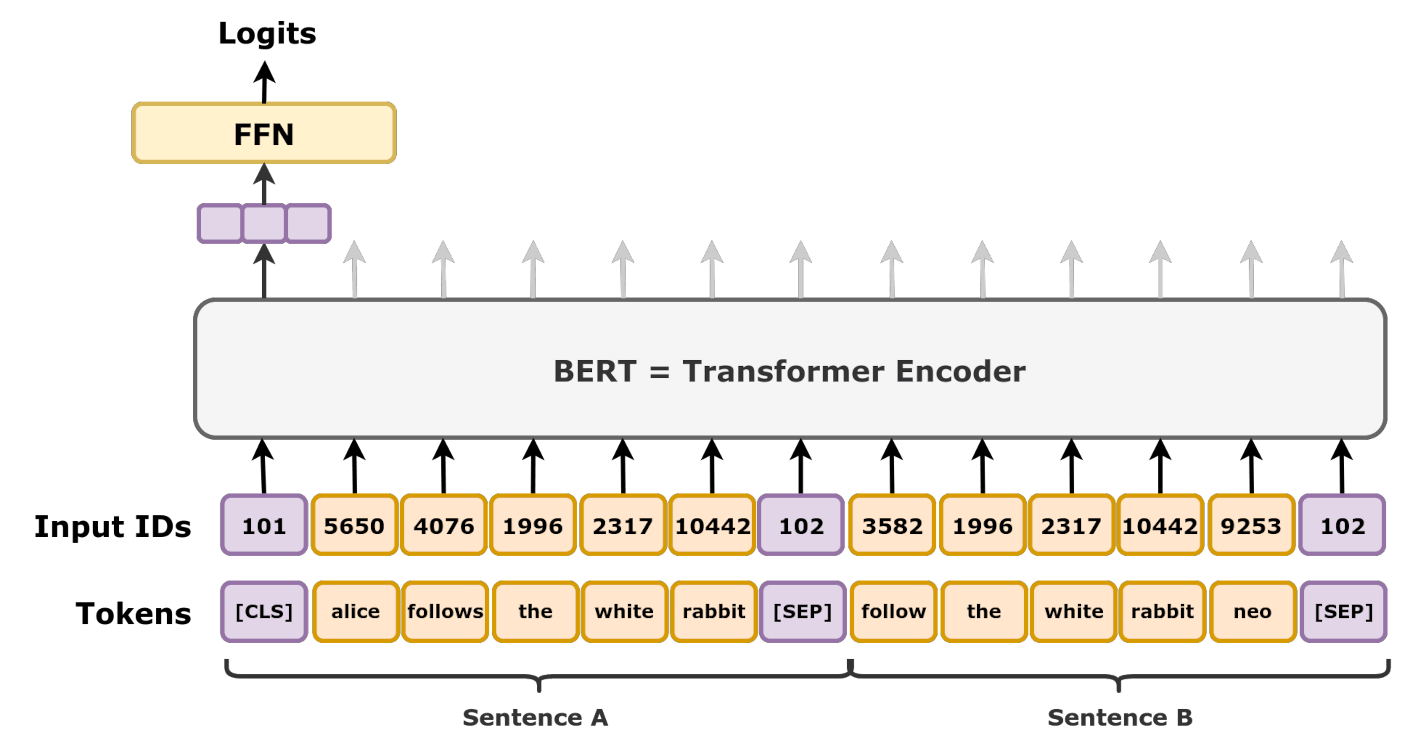
图 37 NSP示意图

\(\hspace{1.5em}\) NSP任务的引入帮助BERT在各种需要句间理解的任务上取得了显著效果。与只关注单句的模型相比，BERT能够更好地捕捉文本中的跨句子逻辑和语义关系，从而更适用于复杂的语言任务。

\(\hspace{1.5em}\) 通过MLM和NSP任务的双重训练，BERT模型在预训练阶段学会了语言中的大量语义和句法结构知识。MLM任务让模型理解了词汇在不同上下文中的意义和作用，NSP任务则帮助模型掌握了句子间的逻辑关系和连贯性。与传统的语言模型相比，BERT在预训练阶段积累了广泛的通用知识，使得它能够被微调到各种不同的下游任务中，如文本分类、命名实体识别、问答系统等。

微调BERT用于情感分析

\(\hspace{1.5em}\) 在本小节中，我们使用 Huggingface 上的IMDB数据集对预训练的 BERT 模型进行微调，以完成情感分析任务。IMDB数据集包含来自互联网电影数据库的电影评论，每条评论都带有情感标签（正面或负面）。为展示微调的效果，我们将考虑以下三种情况：

1. 使用预训练的 BERT 模型，不进行微调；

2. 仅微调预训练 BERT 模型的分类头（classifier）权重；

3. 微调整个预训练的 BERT 模型。

\(\hspace{1.5em}\) 为实现这一任务，我们将按以下步骤进行：

1. 加载IMDB数据集，并使用 BERT 模型的分词器（ tokenizer ）对文本进行 tokenization；

2. 准备 DataLoader 以生成批量数据；

3. 下载 BERT 模型；

4. 在测试集上评估预训练模型性能；

5. 固定模型权重，仅更新分类头权重，并在训练集上训练模型；

6. 在测试集上评估该模型性能；

7. 重新下载 BERT 模型并对整个模型进行微调，并在训练集上训练模型；

8. 在测试集上评估该模型性能。

\(\hspace{1.5em}\) 以下代码展示了如何使用 Huggingface 上的 BERT 模型对IMDB数据集进行情感分析：

# 引入必要的库
import torch
import numpy as np
# 从 ``Huggingface`` 引入Bert模型的Tokenizer和预训练的Bert
from transformers import BertTokenizer, BertForSequenceClassification
from datasets import load_dataset
# DataLoader用于生成batch数据
from torch.utils.data import DataLoader
# 进度条
from tqdm import tqdm

# 设置随机种子
torch.manual_seed(0)
torch.cuda.manual_seed(0)

# 从 ``Huggingface`` 下载imdb数据集
# https:// ``Huggingface`` .co/datasets/stanfordnlp/imdb
imdb_dataset = load_dataset("imdb")

tokenizer = BertTokenizer.from_pretrained("bert-base-uncased")

# Tokenize the dataset
def preprocess_data(examples):
   return tokenizer(examples["text"], truncation=True, padding=True)

encoded_dataset = imdb_dataset.map(preprocess_data, batched=True)

# 获取用于模型训练的训练集和用于测试的测试集
train_dataset = encoded_dataset["train"]
test_dataset = encoded_dataset["test"]

print(test_dataset[0])

\(\hspace{1.5em}\) 上面代码的运行结果如下。从结果中我们可以看到，每个样本包含了 text、label、input_ids、attention_mask 和 token_type_ids 等字段。其中 text 是评论的原始文本，label 是该评论对应的情感标签（0表示负面，1表示正面），input_ids 是经过 tokenizer 处理后得到的 id 序列；attention_mask 表示输入中哪些位置需要忽略（mask），在本例中 <PAD> 部分均需要忽略（值为0）； token_type_ids 是用于区分两个句子的向量，在本例中只有一个句子，因此 token_type_ids 全部为0。

{
   'text': 'I love sci-fi and am willing to put up with a lot. Sci-fi movies/TV are usually underfunded, under-appreciated and misunderstood. I tried to like this, I really did, but it is to good TV sci-fi as Babylon 5 is to Star Trek (the original). Silly prosthetics, cheap cardboard sets, stilted dialogues, CG that doesn\'t match the background, and painfully one-dimensional characters cannot be overcome with a \'sci-fi\' setting. (I\'m sure there are those of you out there who think Babylon 5 is good sci-fi TV. It\'s not. It\'s clichéd and uninspiring.) While US viewers might like emotion and character development, sci-fi is a genre that does not take itself seriously (cf. Star Trek). It may treat important issues, yet not as a serious philosophy. It\'s really difficult to care about the characters here as they are not simply foolish, just missing a spark of life. Their actions and reactions are wooden and predictable, often painful to watch. The makers of Earth KNOW it\'s rubbish as they have to always say "Gene Roddenberry\'s Earth..." otherwise people would not continue watching. Roddenberry\'s ashes must be turning in their orbit as this dull, cheap, poorly edited (watching it without advert breaks really brings this home) trudging Trabant of a show lumbers into space. Spoiler. So, kill off a main character. And then bring him back as another actor. Jeeez! Dallas all over again.',
   'label': 0,
   'input_ids': [101, 1045, 2293, 16596, 1011, 10882, 1998, 2572, 5627, 2000, 2404, 2039, 2007, 1037, 2843, 1012, 16596, 1011, 10882, 5691, 1013, 2694, 2024, 2788, 2104, 11263, 25848, 1010, 2104, 1011, 12315, 1998, 28947, 1012, 1045, 2699, 2000, 2066, 2023, 1010, 1045, 2428, 2106, 1010, 2021, 2009, 2003, 2000, 2204, 2694, 16596, 1011, 10882, 2004, 17690, 1019, 2003, 2000, 2732, 10313, 1006, 1996, 2434, 1007, 1012, 10021, 4013, 3367, 20086, 2015, 1010, 10036, 19747, 4520, 1010, 25931, 3064, 22580, 1010, 1039, 2290, 2008, 2987, 1005, 1056, 2674, 1996, 4281, 1010, 1998, 16267, 2028, 1011, 8789, 3494, 3685, 2022, 9462, 2007, 1037, 1005, 16596, 1011, 10882, 1005, 4292, 1012, 1006, 1045, 1005, 1049, 2469, 2045, 2024, 2216, 1997, 2017, 2041, 2045, 2040, 2228, 17690, 1019, 2003, 2204, 16596, 1011, 10882, 2694, 1012, 2009, 1005, 1055, 2025, 1012, 2009, 1005, 1055, 18856, 17322, 2094, 1998, 4895, 7076, 8197, 4892, 1012, 1007, 2096, 2149, 7193, 2453, 2066, 7603, 1998, 2839, 2458, 1010, 16596, 1011, 10882, 2003, 1037, 6907, 2008, 2515, 2025, 2202, 2993, 5667, 1006, 12935, 1012, 2732, 10313, 1007, 1012, 2009, 2089, 7438, 2590, 3314, 1010, 2664, 2025, 2004, 1037, 3809, 4695, 1012, 2009, 1005, 1055, 2428, 3697, 2000, 2729, 2055, 1996, 3494, 2182, 2004, 2027, 2024, 2025, 3432, 13219, 1010, 2074, 4394, 1037, 12125, 1997, 2166, 1012, 2037, 4506, 1998, 9597, 2024, 4799, 1998, 21425, 1010, 2411, 9145, 2000, 3422, 1012, 1996, 11153, 1997, 3011, 2113, 2009, 1005, 1055, 29132, 2004, 2027, 2031, 2000, 2467, 2360, 1000, 4962, 8473, 4181, 9766, 1005, 1055, 3011, 1012, 1012, 1012, 1000, 4728, 2111, 2052, 2025, 3613, 3666, 1012, 8473, 4181, 9766, 1005, 1055, 11289, 2442, 2022, 3810, 1999, 2037, 8753, 2004, 2023, 10634, 1010, 10036, 1010, 9996, 5493, 1006, 3666, 2009, 2302, 4748, 16874, 7807, 2428, 7545, 2023, 2188, 1007, 19817, 6784, 4726, 19817, 19736, 3372, 1997, 1037, 2265, 13891, 2015, 2046, 2686, 1012, 27594, 2121, 1012, 2061, 1010, 3102, 2125, 1037, 2364, 2839, 1012, 1998, 2059, 3288, 2032, 2067, 2004, 2178, 3364, 1012, 15333, 4402, 2480, 999, 5759, 2035, 2058, 2153, 1012, 102, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
   'token_type_ids': [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
   'attention_mask': [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
}

\(\hspace{1.5em}\) 接下来，我们需要定义两个函数，一个是 eval() 函数，主要用于评估模型在测试集上的性能；另一个是 train() 函数，主要用于训练模型。在 train() 函数中，我们使用 CrossEntropyLoss 作为损失函数，使用 Adam 作为优化器。在训练过程中，我们需要注意以下几点：

1. 在处理每个 batch 数据前，需要将优化器的梯度重置为零；

2. 在 loss.backward() 之后，需要调用 optimizer.step() 更新权重矩阵；

3. 在测试时，需要使用 model.eval()，此时不会计算梯度；

4. 在训练时，需要使用 model.train()，此时需要计算梯度。

# 在train_dataset和test_dataset中，数据类型是list
# 要将数据转换为tensor类型
def collate_fn(batch):
   input_ids = torch.stack([torch.tensor(item['input_ids']) for item in batch])
   attention_mask = torch.stack([torch.tensor(item['attention_mask']) for item in batch])
   labels = torch.tensor([item['label'] for item in batch])
   return {'input_ids': input_ids, 'attention_mask': attention_mask, 'labels': labels}

# train_dataloader将原始数据集生成batch数据
# batch_size 设为 32
test_dataloader = DataLoader(test_dataset, batch_size=32, shuffle=True, collate_fn=collate_fn)
train_dataloader = DataLoader(train_dataset, batch_size=32, shuffle=True, collate_fn=collate_fn)

# 测试模型在数据集上的准确率
def eval(model, dataloader, device):
   total_correct = 0
   total_examples = 0
   # 使用GPU
   model = model.to(device)
   # 在测试时，需要使用model.eval()
   # 此时不会计算梯度
   model.eval()

   # !!! 测试时不需要计算梯度
   with torch.no_grad():
      for batch in tqdm(dataloader):
            input_ids = batch["input_ids"].to(device)
            attention_mask = batch["attention_mask"].to(device)
            labels = batch["labels"].to(device)

            # 前向传播，得到预测的标签
            # outputs = [batch, label]
            outputs = model(input_ids, attention_mask=attention_mask)
            predictions = outputs.logits.argmax(dim=-1)
            correct = (predictions == labels).sum().item()
            total_correct += correct
            total_examples += labels.size(0)

   # 打印预测精度
   print(f"Accuracy: {total_correct / total_examples}")

# 给定训练集，训练模型
def train(model, dataloader, device):
   # loss function
   criterion = torch.nn.CrossEntropyLoss()
   # 优化器
   # 实际应用中，learning rate是一个超参数
   optimizer = torch.optim.Adam(model.parameters(), lr=1e-5)
   # 使用GPU
   model = model.to(device)

   # 模型训练5个epoch
   for epoch in range(5):
      total_loss = 0
      total_correct = 0
      total_examples = 0
      # 模型训练时需要计算梯度
      model.train()

      for batch in tqdm(dataloader):
            # !!! 对优化器中的梯度重置
            optimizer.zero_grad()
            input_ids = batch["input_ids"].to(device)
            attention_mask = batch["attention_mask"].to(device)
            labels = batch["labels"].to(device)

            # 前向传播
            outputs = model(input_ids, attention_mask=attention_mask)
            loss = criterion(outputs.logits, labels)
            total_loss += loss.item()

            # 反向传播的计算方式
            loss.backward()
            # 更新权重矩阵
            optimizer.step()

            # 计算准确率和cost function
            predictions = outputs.logits.argmax(dim=-1)
            correct = (predictions == labels).sum().item()
            total_correct += correct
            total_examples += labels.size(0)

      print(f"Epoch {epoch} Loss: {total_loss / len(dataloader)}, Accuracy: {total_correct / total_examples}")

   # 返回训练过后的模型
   return model

\(\hspace{1.5em}\) 在进行微调时，我们需要考虑哪些参数是需要固定的（不需要进行梯度更新，所以 requires_grad = False），哪些需要训练（requires_grad = True）。下面，我们定义两个函数 frozen() 和 num_paras()，分别用于固定模型中的某些参数和计算模型中的全部参数和可训练的参数。

# 如果想要让模型只训练classifier
# 可以将Bert模型中的参数设置为不需要梯度
# 此步骤也可以设置Bert中的某些层不需要梯度
def frozen(model):
   for name, param in model.named_parameters():
      # 除了分类器中的参与以外，其他参数均不需要计算梯度
      if 'classifier' not in name:
            param.requires_grad = False
   return model

# 计算模型中的全部参数和可训练（requires_grad=True）的参数
def num_paras(model):
   total_paras = model.parameters()
   train_paras = filter(lambda p: p.requires_grad, model.parameters())
   total_num_params = sum([np.prod(p.size()) for p in total_paras])
   train_num_params = sum([np.prod(p.size()) for p in train_paras])

   return total_num_params, train_num_params

\(\hspace{1.5em}\) 下面，我们从 bert-base-uncased 模型中加载预训练的模型，并查看模型的结构。

# 根据情况设置是否使用GPU
# 如果是在kaggle、colab或者天池平台，请确保已经打开GPU加速选项
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

# 下载预训练的模型
# 其中classifier部分的权重矩阵和偏置项仅初始化（没有训练过）
# BertForSequenceClassification类中，封装了一个classifier
# 这一步也可以手动增加一个 nn.Linear(768, 2) 实现
pre_trained_model = BertForSequenceClassification.from_pretrained("bert-base-uncased", num_labels=2)

print(pre_trained_model)

total_paras_pre_trained, train_paras_pre_trained = num_paras(pre_trained_model)
print(f'预训练模型中一共有 {total_paras_pre_trained} 个参数，其中 {train_paras_pre_trained} 个参数是可训练的')

\(\hspace{1.5em}\) 以下为代码的运行结果。从中我们可以看到，BertForSequenceClassification 返回的结果是一个BERT模型 (bert): BertModel() 和一个分类器 (classifier)。其中，BERT的权重是预训练的，而分类器的权重是随机初始化的，一共有 109483778 个参数。对于BERT模型，包含了 (embeddings) 层、(encoder) 层，以及 (pooler) 层。其中 (embeddings) 层主要是将输入的token转换为向量表示，包括 word_embeddings、position_embeddings 和 token_type_embeddings。 (encoder) 层是BERT的核心部分，包含了 12 个 BertLayer，每个层与 Transformer 中的编码器使用了相同的结构，(pooler) 层是BERT的输出层，将BERT的输出转换为分类器的输入。

Some weights of BertForSequenceClassification were not initialized from the model checkpoint at bert-base-uncased and are newly initialized: ['classifier.bias', 'classifier.weight']

You should probably TRAIN this model on a down-stream task to be able to use it for predictions and inference.
BertForSequenceClassification(
   (bert): BertModel(
      (embeddings): BertEmbeddings(
         (word_embeddings): Embedding(30522, 768, padding_idx=0)
         (position_embeddings): Embedding(512, 768)
         (token_type_embeddings): Embedding(2, 768)
         (LayerNorm): LayerNorm((768,), eps=1e-12, elementwise_affine=True)
         (dropout): Dropout(p=0.1, inplace=False)
      )
      (encoder): BertEncoder(
         (layer): ModuleList(
         (0-11): 12 x BertLayer(
            (attention): BertAttention(
               (self): BertSdpaSelfAttention(
               (query): Linear(in_features=768, out_features=768, bias=True)
               (key): Linear(in_features=768, out_features=768, bias=True)
               (value): Linear(in_features=768, out_features=768, bias=True)
               (dropout): Dropout(p=0.1, inplace=False)
               )
               (output): BertSelfOutput(
               (dense): Linear(in_features=768, out_features=768, bias=True)
               (LayerNorm): LayerNorm((768,), eps=1e-12, elementwise_affine=True)
               (dropout): Dropout(p=0.1, inplace=False)
               )
            )
            (intermediate): BertIntermediate(
               (dense): Linear(in_features=768, out_features=3072, bias=True)
               (intermediate_act_fn): GELUActivation()
            )
            (output): BertOutput(
               (dense): Linear(in_features=3072, out_features=768, bias=True)
               (LayerNorm): LayerNorm((768,), eps=1e-12, elementwise_affine=True)
               (dropout): Dropout(p=0.1, inplace=False)
            )
         )
         )
      )
      (pooler): BertPooler(
         (dense): Linear(in_features=768, out_features=768, bias=True)
         (activation): Tanh()
      )
   )
   (dropout): Dropout(p=0.1, inplace=False)
   (classifier): Linear(in_features=768, out_features=2, bias=True)
)
预训练模型中一共有 109483778 个参数，其中 109483778 个参数是可训练的

\(\hspace{1.5em}\) 接下来，我们看看预训练模型（pre-trained model）在测试集上的准确率。

# 查看预训练模型在测试集上的准确率
print("预训练模型（pre-trained model）在测试集上的准确率为：")
eval(pre_trained_model, test_dataloader, device)

\(\hspace{1.5em}\) 我们发现，预训练模型在测试集上的准确率为 0.4968，这是因为分类器的权重是随机初始化的，所以此时模型在进行预测时就和抛硬币（random guess）差不多。

预训练模型（pre-trained model）在测试集上的准确率为：
100%|██████████| 782/782 [06:53<00:00,  1.89it/s]
Accuracy: 0.4968

\(\hspace{1.5em}\) 接下来，我们将预训练模型中的权重固定，仅更新分类器的权重，然后利用训练集进行训练。

# 将预训练模型中的权重固定
# 仅考虑更新分类器的权重
print("固定预训练模型的权重")
frozen_model = frozen(pre_trained_model)

total_paras_pre_trained, train_paras_pre_trained = num_paras(frozen_model)
print(f'固定权重模型中一共有 {total_paras_pre_trained} 个参数，其中 {train_paras_pre_trained} 个参数是可训练的')

# 模型训练
print("对固定权重的模型进行训练（仅更新分类器）")
trained_frozen_model = train(frozen_model, train_dataloader, device)

# 模型测试
print("训练后模型（frozen model）在测试集上的准确率为：")
eval(trained_frozen_model, test_dataloader, device)

\(\hspace{1.5em}\) 经过 5 个 epoch 的训练，我们发现 frozen model 在测试集上的准确率为 0.66948。

固定预训练模型的权重
固定权重模型中一共有 109483778 个参数，其中 1538 个参数是可训练的

对固定权重的模型进行训练（仅更新分类器）

100%|██████████| 782/782 [07:13<00:00,  1.80it/s]
Epoch 0 Loss: 0.6914244227854492, Accuracy: 0.52492
100%|██████████| 782/782 [07:13<00:00,  1.80it/s]
Epoch 1 Loss: 0.6801337108130345, Accuracy: 0.56936
100%|██████████| 782/782 [07:13<00:00,  1.80it/s]
Epoch 2 Loss: 0.6709886162787142, Accuracy: 0.6006
100%|██████████| 782/782 [07:13<00:00,  1.80it/s]
Epoch 3 Loss: 0.663662817929407, Accuracy: 0.61896
100%|██████████| 782/782 [07:13<00:00,  1.80it/s]
Epoch 4 Loss: 0.6565081448201329, Accuracy: 0.6326

训练后模型（frozen model）在测试集上的准确率为：
100%|██████████| 782/782 [06:54<00:00,  1.89it/s]
Accuracy: 0.66948

\(\hspace{1.5em}\) 最后，我们重新下载预训练模型，整个模型的权重都更新，然后利用训练集进行训练。

# 下载预训练模型
# !!! 我们是重新下载预训练的模型
# 而不是使用 trained_frozen_model
pre_trained_model_full = BertForSequenceClassification.from_pretrained("bert-base-uncased", num_labels=2)

# 同时更新整个模型的权重
print("对整个模型进行训练（所有参数均会更新）")
trained_full_model = train(pre_trained_model_full, train_dataloader, device)

# 模型测试
print("训练后模型（full model）在测试集上的准确率为：")
eval(trained_full_model, test_dataloader, device)

\(\hspace{1.5em}\) 经过 5 个 epoch 的训练，我们发现 full model 在测试集上的准确率为 0.93832。

Some weights of BertForSequenceClassification were not initialized from the model checkpoint at bert-base-uncased and are newly initialized: ['classifier.bias', 'classifier.weight']
You should probably TRAIN this model on a down-stream task to be able to use it for predictions and inference.
对整个模型进行训练（所有参数均会更新）

100%|██████████| 782/782 [22:05<00:00,  1.69s/it]
Epoch 0 Loss: 0.26227911953311744, Accuracy: 0.89172
100%|██████████| 782/782 [22:05<00:00,  1.70s/it]
Epoch 1 Loss: 0.14827332975547713, Accuracy: 0.94592
100%|██████████| 782/782 [22:06<00:00,  1.70s/it]
Epoch 2 Loss: 0.09031119023252021, Accuracy: 0.9704
100%|██████████| 782/782 [22:06<00:00,  1.70s/it]
Epoch 3 Loss: 0.05729520047033477, Accuracy: 0.98276
100%|██████████| 782/782 [22:06<00:00,  1.70s/it]
Epoch 4 Loss: 0.04181397326982549, Accuracy: 0.98796

训练后模型（full model）在测试集上的准确率为：
100%|██████████| 782/782 [06:54<00:00,  1.88it/s]
Accuracy: 0.93832

\(\hspace{1.5em}\) 由此可见，微调显著提高了模型在测试集上的准确率。在实际应用中，我们可以根据任务需求选择是否固定预训练模型的权重，或者更新整个模型。对于一些应用，可以固定预训练模型权重，只更新分类器，以节省训练时间和计算资源；而在其他需要更高精度的任务中，则可以更新整个模型的权重来获得更好的表现。

如何选择超参数

\(\hspace{1.5em}\) 在上述示例中，我们使用了默认的超参数值，例如 batch_size=32 和 lr=1e-5。尽管这些值在一般情况下可以有效，但它们未必适用于所有任务或数据集。为了找到最优的超参数组合，我们通常需要进行调参（hyper-parameters tuning），最常用的方式之一就是将训练数据集（training set）划分出一部分作为验证集（validation set），然后使用不同的超参数组合来训练模型，并在验证集上评估每种组合的效果。这一过程帮助我们识别出在验证集上表现最好的超参数组合，而非依赖于单一的默认值。超参数调整的一些常用策略包括以下几种：

• 网格搜索（Grid Search）：选择多个候选值，并尝试所有可能的组合，例如对 batch_size 设置多个可能值如 16、32、64，对学习率（lr）设置如 1e-5、3e-5、5e-5，然后测试所有组合，找到验证集上效果最佳的组合。虽然简单，但网格搜索在维度较高的超参数空间中计算量较大。

• 随机搜索（Random Search）：随机选择一些超参数组合进行尝试，相较于网格搜索能节省时间，在较大参数空间中往往能找到不错的超参数组合。

• 贝叶斯优化（Bayesian Optimization）：基于先前尝试过的组合，不断更新选择的策略，逐步找到最优超参数。贝叶斯优化计算效率更高，适用于高维度和资源受限的场景。