循环神经网络的变种#
\(\hspace{1.5em}\) 在上一节中,我计算了RNN中梯度的反向传播过程。在时间步 \(t\),所有 \(\tau > t\) 时刻的梯度会通过各个隐藏状态 \(h_{t + i} (i = \tau, \tau-1, \dots, 1)\) 向 \(h_t\) 反向传播。然而,由于包含连乘项 \((\Pi_{i=t+1}^{\tau} \frac{\partial h_{i}}{\partial h_{i-1}})\),梯度随着时间步的增加会呈指数级衰减或增长,导致梯度消失或爆炸。为了应对梯度消失问题,Hochreiter和Schmidhuber(1997) 提出了一种利用门控机制(gate mechanism)来控制信息流动的方法。接下来,我们将介绍两种广泛使用的门控循环神经网络变体——长短期记忆网络(LSTM)和门控循环单元(GRU),并解释门控机制如何帮助缓解梯度消失问题。
长短期记忆网络(LSTM)#
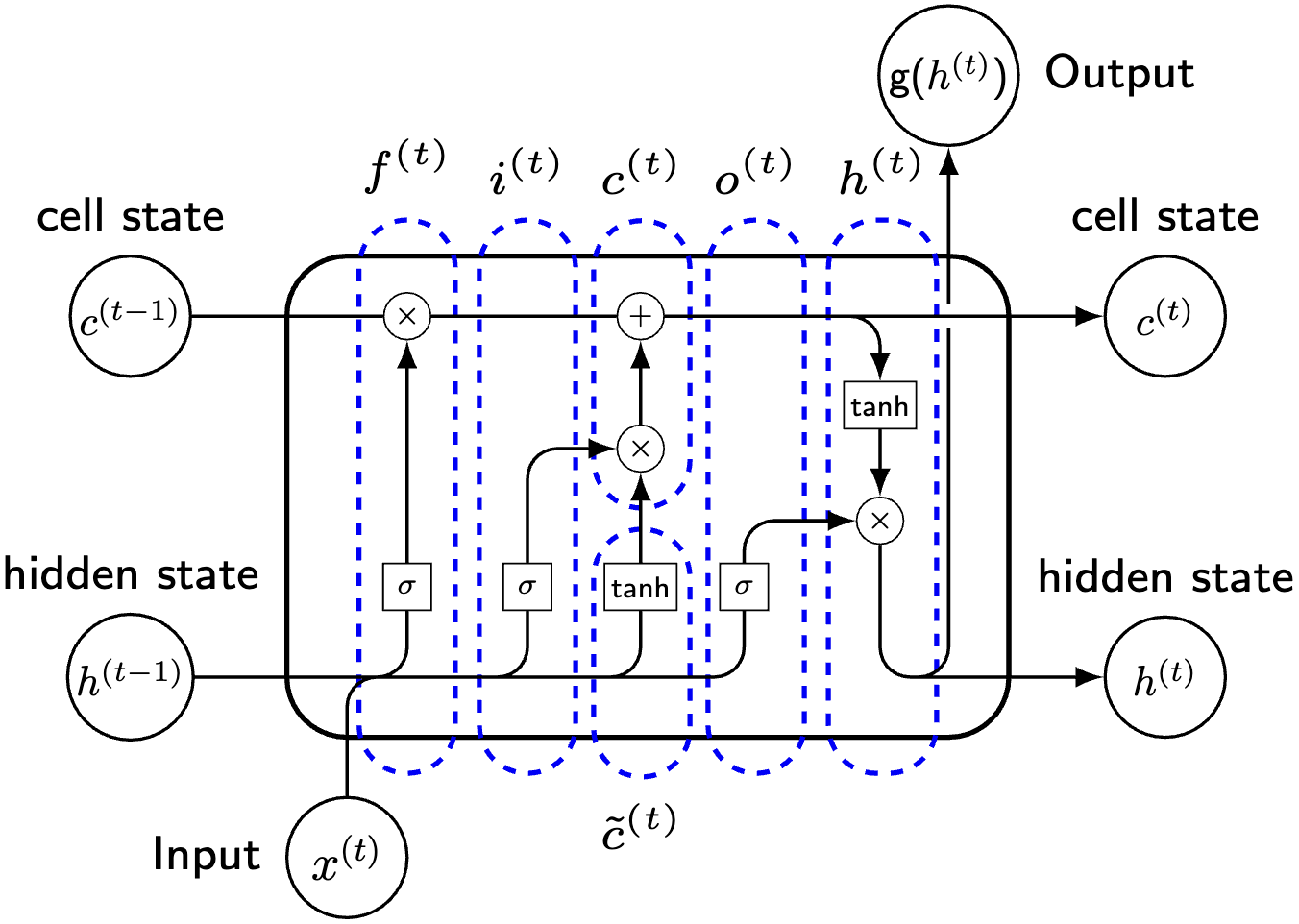
LSTM单元的基本结构#
\(\hspace{1.5em}\) 长短期记忆网络(Long Short-Term Memory,LSTM)是一种特殊的循环神经网络(RNNs),它通过引入三个门控单元来控制信息的流动。LSTM中每个单元的计算公式如下 1这里我们忽略了从隐藏状态 \(h_t\) 到输出 \(y_t\) 的计算,因为这部分和RNN是一样的。在LSTM中,我们主要关注单元状态 \(c_t\) 和隐藏状态 \(h_t\) 的计算。:
其中,\(\odot\) 表示 Hadamard 积(逐元素乘积,elementwise product),\(b_i, b_f, b_o, b_c \in \mathcal{R}^{d_h}\) 分别对应于输入门、遗忘门、输出门和单元状态的偏置项。这里,\(d_i\) 和 \(d_h\) 分别表示输入和隐藏状态的维度。通常情况下,\(i_t, f_t, o_t \in \mathcal{R}^{d_h}\) 分别称为输入门、遗忘门和输出门的激活值,\(\tilde c_t \in \mathcal{R}^{d_h}\) 表示候选单元状态,\(c_t \in \mathcal{R}^{d_h}\) 为单元状态,即 LSTM 的内部记忆,而 \(h_t \in \mathcal{R}^{d_h}\) 是LSTM的隐藏状态,也是网络的输出。各权重矩阵和偏置项定义如下:\(W_{ix} \in \mathcal{R}^{d_h \times d_i}\) 和 \(W_{ih} \in \mathcal{R}^{d_h \times d_h}\) 是输入门的权重,\(W_{fx} \in \mathcal{R}^{d_h \times d_i}\) 和 \(W_{fh} \in \mathcal{R}^{d_h \times d_h}\) 是遗忘门的权重,\(W_{ox} \in \mathcal{R}^{d_h \times d_i}\) 和 \(W_{oh} \in \mathcal{R}^{d_h \times d_h}\) 是输出门的权重,\(W_{cx} \in \mathcal{R}^{d_h \times d_i}\) 和 \(W_{ch} \in \mathcal{R}^{d_h \times d_h}\) 是单元状态的权重。
\(\hspace{1.5em}\) 我们首先根据更新方程来理解LSTM的基本构造。首先,LSTM 中的三个门控单元 \(i_t\)、\(f_t\) 和 \(o_t\) 的计算方式是相同的(权重矩阵不同)。每个门控单元通过与输入和前一隐藏状态的线性组合并施加激活函数来得到。这三个向量中每一个元素的值域都在 \((0, 1)\) 之间,因此我们可以将他们看作是权重。
\(\hspace{1.5em}\) 与RNN不同,LSTM中额外增加了一个单元状态(cell state)。从更新方程中我们可以发现,\(\tilde c_t\) 的计算与RNN中隐藏状态的计算方式完全一致,我们可以将LSTM中的候选单元状态与RNN中的隐藏状态作为类比,看作是历史信息的潜在表示。对于单元状态 \(c_t\) 的计算,可以看作是对于历史信息的更新(加权求和)。通过遗忘门 \(f_t\) 控制历史信息 \(c_{t-1}\) 的保留程度,通过输入门 \(i_t\) 控制新信息 \(\tilde c_t\) 的输入。这样的好处在于,在第 \(k\) 个维度,历史信息可以完全保留( \(f_{t, k} = 1\) )或者完全遗忘( \(f_{t, k} = 0\)),新信息可以完全输入( \(i_{t, k} = 1\) )或者完全忽略( \(i_{t, k} = 0\))。与RNN中隐藏状态的计算相比,LSTM中单元状态的更新多了一步与历史信息的加权求和,这使得LSTM能够更好的保留重要的历史信息。如果我们将 \(\tilde c_t\) 看作是短期记忆(因为仅考虑了 \(h_{t-1}\)),那么 \(c_t\) 可以看作是长期记忆,通过这个加权求和,实现了对历史信息的长期记忆,这也是LSTM名字的由来(Long Short-Term Memory : make the short-term memory long)。
\(\hspace{1.5em}\) 在LSTM中,同样使用了一个隐藏状态 \(h_t\)。从 \(h_t\) 的计算方程来看,我们可以将其视作是单元状态 \(c_t\) 的一个可输出表示,这是因为输出门 \(0 < o_{t, k} < 1\) 控制了单元状态的输出到隐藏状态 \(h_t\) 的过程,即从 \(c_t\) 中提取了与输出有关的信息。
门控循环单元(GRU)#

RNN的基本结构#
\(\hspace{1.5em}\) 门控循环单元(Gated Recurrent Unit,GRU)是另一种使用了门控机制的循环神经网络(RNNs),它通过引入两个门控单元来控制信息的流动。GRU的计算公式如下:
其中 \(u_t \in \mathcal{R}^{d_h}\) 和 \(r_t \in \mathcal{R}^{d_h}\) 分别是更新门和重置门的激活值,\(\tilde h_t \in \mathcal{R}^{d_h}\) 是候选隐藏状态,\(h_t \in \mathcal{R}^{d_h}\) 是隐藏状态;\(W_{ux} \in \mathcal{R}^{d_h \times d_i}\) 和 \(W_{uh} \in \mathcal{R}^{d_h \times d_h}\) 是更新门权重,\(W_{rx} \in \mathcal{R}^{d_h \times d_i}\) 和 \(W_{rh} \in \mathcal{R}^{d_h \times d_h}\) 是重置门权重,\(W_{hx} \in \mathcal{R}^{d_h \times d_i}\) 和 \(W_{hh} \in \mathcal{R}^{d_h \times d_h}\) 是候选隐藏状态的权重。
\(\hspace{1.5em}\) 在GRU中同样使用了门控机制,可以看作是LSTM的一个简化版本。与LSTM不同的是,GRU中只有一个隐藏状态 \(h_t\),而没有单元状态 \(c_t\)。GRU 的门控机制包含两个门:更新门 \(u_t\) 和重置门 \(r_t\),它们的计算方式与 LSTM 中的门控单元相似。更新门 \(u_t\) 控制历史信息和新信息的融合比例,而重置门 \(r_t\) 决定历史信息的保留程度。候选隐藏状态 \(\tilde{h}_t\) 则通过前一时刻的历史信息 \(h_{t-1}\) 和当前输入 \(x_t\) 计算得出,其中 \(r_t \odot W_{hh} h_{t-1}\) 可与 LSTM 中的 \(f_t \odot c_{t-1}\) 类比,用于调控历史信息的保留比例。GRU中隐藏状态的计算与LSTM中的隐藏状态计算类似,但是没有了单元状态的概念,因此隐藏状态 \(h_t\) 既是网络的输出,也是网络的内部记忆。
LSTM v.s. GRU#
\(\hspace{1.5em}\) 在RNN中,隐藏状态可以被视为目标序列的潜在表示。LSTM引入了一个单独的单元状态(Cell state)来保存历史信息,它作为时间 \(t\) 前所有信息的摘要。相比之下,GRU直接利用隐藏状态来结合历史信息。这种方法不仅减少了所需的参数数量,例如LSTM中的输出门 \(o_{t}\),还缓解了将单元状态转换为隐藏状态时产生的偏差(bias)。
\(\hspace{1.5em}\) 除了在表示历史信息方式上的区别,这两种模型在门控机制的使用上也有所不同。例如,LSTM分别使用输入门和遗忘门 \(i_{t}\) 和 \(f_{t}\) 来确定历史信息 \(c_{t-1}\) 与新信息 \(\tilde c_{t}\) 之间的权重。这种方法可能导致当 \(i_{t}\) 和 \(f_{t}\) 取极端值时,单元状态 \(c_{t}\) 变得难以解释 2例如,当 \(i_{t, k} = f_{t, k} = 0 \in \mathcal{R}^{d_h}\) 时,\(c_{t, k} = 0\)。。相比之下,GRU使用更新门 \(u_{t}\) (及其补数 \(\textbf{1} - u_{t}\))作为权重,确保隐藏状态 \(h_{t}\) 仅由历史信息 \(h_{t-1}\) 和新信息 \(\tilde h_{t}\) 决定。当 \(u_{t, k}\) 接近于0时,表明新信息比历史信息更为重要,且 \(h_{t}\) 完全由 \(\tilde h_{t}\) 决定。然而,鉴于序列建模中的自相关衰减现象,GRU还引入了重置门 \(r_{t}\) 来保留历史信息。该门可以被解释为ARMA模型中的AR系数,功能上类似于LSTM中的遗忘门 \(f_{t}\)。重置门决定了要保留多少历史信息,以生成候选隐藏状态 \(\tilde h_{t}\)。这可以视为一种双重保险,利用了序列中存在的强相关性。
\(\hspace{1.5em}\) 从更新方程上来看,GRU的参数更少,因此计算效率更高。在实际应用中,LSTM和GRU在许多数据集上具有相同的效果(comparable performance)。
门控机制有什么用?#
\(\hspace{1.5em}\) 在RNN的BPTT中,我们发现,梯度消失或者爆炸主要的原因在于 \(\frac{\partial \mathcal{J}}{\partial h_t}\) 中会出现连乘项 \(\Pi_{i=t+1}^{\tau} \frac{\partial h_{i}}{\partial h_{i-1}}\) 。由于GRU与RNN相同,使用了隐藏状态作为历史信息的潜在表示,同时,GRU和LSTM相比更简单,所以我们以一个简化的GRU模型为例来说明门控机制在BPTT中的作用。
\(\hspace{1.5em}\) 为了简化计算,不失一般性地,我们将激活函数设为 identity 函数:\(\sigma(x) = x\),同时忽略偏置项。由于GRU中门控单元的计算也会包括 \(x_t\) 和 \(h_{t-1}\),这会让我们的计算变得复杂。因此,在这里我们考虑门控单元为常数,即 \(u_t = D_u\) 和 \(r_t = D_r\),其中 \(D_u\) 和 \(D_r\) 是一个对角矩阵,每个对角元素都是常数。这样我们可以将 \(h_t\) 的计算简化为:
\(\hspace{1.5em}\) 我们可以对 () 进行进一步化简:
\(\hspace{1.5em}\) 此时,根据链式法则,我们有:
\(\hspace{1.5em}\) 值得注意的是,\(D_u\) 和 \(D_r\) 中对角元素的值域都在 \((0, 1)\) 之间。为了更进一步理解门控机制的作用,我们可以考虑几种极端情况:
当 \(D_u = 0\) 时, \(h_t = h_{t-1}\),即历史信息完全保留,新信息完全忽略。此时梯度 \(\frac{\partial h_{t}}{\partial h_{t-1}} = I\),连乘项不会为0;
当 \(D_u = 1, D_r = 0\) 时,\(h_t = \tilde h_t = W_{hx} x_t\),即历史信息完全忽略,新信息完全保留;此时梯度 \(\frac{\partial h_{t}}{\partial h_{t-1}} = 0\),由于此时历史信息和未来信息之间没有任何联系,因此梯度(正常)消失;
当 \(D_u = 1, D_r = 1\) 时,\(h_t = W_{hx} x_t + W_{hh} h_{t-1}\),此时更新方程与RNN相同;
当 \(D_u\) 和 \(D_r\) 的取值在 \((0, 1)\) 之间时,我们可以看到,门控机制 缓解 3虽然LSTM和GRU声称(claim)解决了梯度消失的问题,但实际上只是缓解了这个问题。感兴趣的同学可以参考文章: Do RNN and LSTM have Long Memory? 。 了连乘项 \({\color{red}{(W_{hh}^{\top})^{\tau - t}}}\) 带来的问题。