循环神经网络（Recurrent Neural Networks, RNNs）

\[ \begin{align}\begin{aligned}\newcommand{\ba}{\boldsymbol{a}} \newcommand{\bb}{\boldsymbol{b}} \newcommand{\be}{\boldsymbol{e}} \newcommand{\bw}{\boldsymbol{w}} \newcommand{\bx}{\boldsymbol{x}} \newcommand{\by}{\boldsymbol{y}} \newcommand{\bz}{\boldsymbol{z}} \newcommand{\bd}{\boldsymbol{d}} \newcommand{\bv}{\boldsymbol{v}} \newcommand{\bs}{\boldsymbol{s}}\\\newcommand{\btheta}{\boldsymbol{\theta}} \newcommand{\bbeta}{\boldsymbol{\beta}} \newcommand{\bgamma}{\boldsymbol{\gamma}} \newcommand{\bsigma}{\boldsymbol{\sigma}} \newcommand{\md}{\mbox{d}} \newcommand{\bmu}{\boldsymbol{\mu}} \newcommand{\bone}{\boldsymbol{1}} \newcommand{\trans}{^{\rm\scriptsize T}} \newcommand{\var}{\mathrm{var}}\\\newcommand{\bA}{\boldsymbol{A}} \newcommand{\bB}{\boldsymbol{B}} \newcommand{\bC}{\boldsymbol{C}} \newcommand{\bD}{\boldsymbol{D}} \newcommand{\bI}{\boldsymbol{I}} \newcommand{\bM}{\boldsymbol{M}} \newcommand{\bW}{\boldsymbol{W}} \newcommand{\bX}{\boldsymbol{X}} \newcommand{\bY}{\boldsymbol{Y}} \newcommand{\bZ}{\boldsymbol{Z}} \newcommand{\cotp}{\textcolor{ #30D158FF }{TP}} \newcommand{\cotn}{\textcolor{#64D2FFFF}{TN}} \newcommand{\cofp}{\textcolor{#5E5CE6FF}{FP}} \newcommand{\cofn}{\textcolor{#BF5AF2FF}{FN}}\\\newcommand{\numcotp}{\textcolor{ #30D158FF }{50}} \newcommand{\numcotn}{\textcolor{#64D2FFFF}{30}} \newcommand{\numcofp}{\textcolor{#5E5CE6FF}{10}} \newcommand{\numcofn}{\textcolor{#BF5AF2FF}{10}}\end{aligned}\end{align} \]
1“循环神经网络（Recurrent Neural Networks， RNNs）”泛指一类模型，这些模型具有相同的循环结构，区别在于每个模型的循环单元（Cell structure）不同；而“循环神经网络（Recurrent Neural Network， RNN）”通常特指最基本的循环神经网络模型（Vanilla RNN）。在本章中，我们统一用循环神经网络代表这一类模型，而用RNN特指Vanilla RNN模型。

循环神经网络（Recurrent Neural Networks, RNNs） 1“循环神经网络（Recurrent Neural Networks， RNNs）”泛指一类模型，这些模型具有相同的循环结构，区别在于每个模型的循环单元（Cell structure）不同；而“循环神经网络（Recurrent Neural Network， RNN）”通常特指最基本的循环神经网络模型（Vanilla RNN）。在本章中，我们统一用循环神经网络代表这一类模型，而用RNN特指Vanilla RNN模型。#

\(\hspace{1.5em}\) 在引言中，我们认识到，选择合适的模型在数据建模过程中至关重要。对于静态数据（如图像和表格数据），由于不涉及时间顺序，可以使用多层感知机（MLP）或卷积神经网络（CNN）进行建模。然而，对于序列数据而言，输入数据的顺序尤为重要。例如在时间序列数据（如股票价格、气象数据）和文本数据（如句子、对话）中，当前观测值通常与历史观测值密切相关。接下来，我们将以时间序列预测和语言模型这两个经典问题为切入点，去理解循环神经网络（RNN）的基本思想和原理。

循环神经网络（Vanilla RNN）#

\(\hspace{1.5em}\) 如何才能让神经网络有效地对序列数据进行建模呢？从前两节内容中我们可以看出，序列数据的核心特征是“ 时间依赖性 ”，即输出不仅依赖于当前的输入，还与历史数据密切相关。在前面讨论中我们提到，从线性回归模型发展到自回归模型的关键转变在于，将滞后阶变量（lagged variables）作为自变量引入模型。此外，许多序列数据还具备一个重要性质，即马尔可夫性质：当前观测值仅与前一个或前几个观测值相关。也就是说，\(P(x_t | x_{t-1}, ..., x_{1}) = P(x_t | x_{t-1})\) 或者 \(P(x_t | x_{t-1}, ..., x_{1}) = P(x_t | x_{t-1}, x_{t-2}, ..., x_{t-P})\)。基于此，一个简单的想法是，像自回归模型一样，将前 \(P\) 个观测值输入神经网络中，以便输出预测值 \(\hat x_t\)，从而让网络“利用”历史信息来更好地捕捉序列数据中的时间相依性。

\(\hspace{1.5em}\) 然而，这种方法存在多个问题：

  1. 模型是否满足马尔可夫性？模型满足几阶马尔可夫性？也就是说，我们无法确定模型的滞后阶数（即需要考虑多少个历史观测值）。

  2. 模型参数数量会随滞后阶数的增加而增长，导致模型复杂度和训练难度显著增加。

  3. 由于MLP的输入维度是固定的，因此无法处理变长的序列数据。

\(\hspace{1.5em}\) 有没有更好的方法呢？回到问题的本质，我们希望能保留和利用历史信息。然而，历史信息本质上是一个难以精确捕捉的概念。最理想的历史信息当然是所有真实的历史观测值，但直接将这些信息输入神经网络是不现实的。为此，研究者们引入了一个巧妙的替代方案：用一个隐藏状态（hidden state）来近似历史信息。即

\[P(x_t | x_{t-1}, ..., x_{1}) \approx P(x_t | h_{t-1}).\]

\(\hspace{1.5em}\) 从直观上看，我们可以将隐藏状态视为历史信息在一个不可直接观测的空间（latent space）中的抽象表达。在每个时刻 \(t\)，神经网络接收当前输入 \(x_t\) 和前一时刻的隐藏状态 \(h_{t-1}\)，其中 \(h_{t-1}\) 包含了时刻 \(t\) 之前所有的历史信息。数据经过神经网络后，我们得到最新的隐藏状态 \(h_t\)，该隐藏状态在 \(h_{t-1}\) 的基础上增加了 \(x_t\) 的信息。通过这种方式，我们便可以不断对历史信息进行保留（利用）和更新。

\(\hspace{1.5em}\) 接下来，我们给出 RNNs 的基本结构：

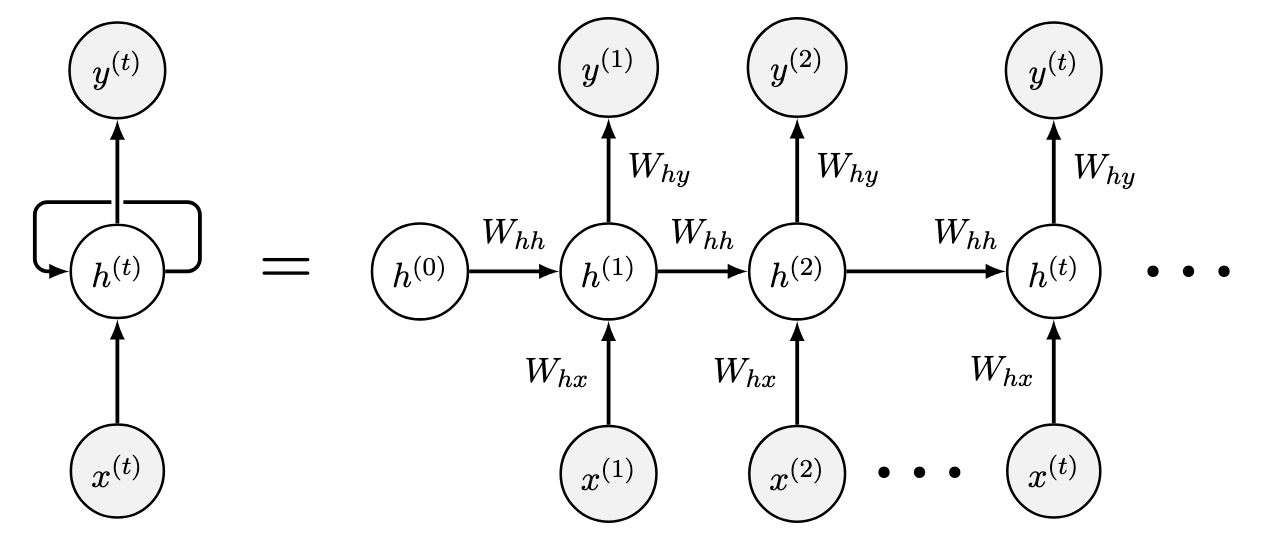
../_images/Figure_6_3_RNN.png

Vanilla RNN的基本结构#

\(\hspace{1.5em}\) 图中左侧部分展示了 RNNs 的基本结构，其中 \(h_t\) 部分为循环单元（recurrent unit or cell unit），通过结合当前时刻输入与前一时刻的隐藏状态，对当前时刻的隐藏状态进行更新。这个反馈结构使得历史信息能够逐步传递到当前时刻，避免了模型定阶的问题。上图右侧部分展示了模型在时间步 \(t\) 的具体更新过程。对于所有 RNNs 来说，这个反馈结构都是相同的，不同点在于循环单元的具体形式。在 Vanilla RNN 中，循环单元的更新方程如下：

()#\[\begin{split}h_t &= \tanh(W_{hh} h_{t-1} + W_{{hx}} x_t + b_h)\\ y_t &= \sigma(W_{{yh}} h_t + b_y).\end{split}\]

更新方程 () 描述了RNN在时刻 \(t\) 的计算过程。设输入、输出和隐藏状态的维度分别为 \(d_i, d_o, d_h\)，其中输入 \(x_t \in \mathcal{R}^{d_i}\)，输出 \(y_t \in \mathcal{R}^{d_o}\)，隐藏状态 \(h_t \in \mathcal{R}^{d_h}\)。模型的权重矩阵为 \(W_{hh} \in \mathcal{R}^{d_h \times d_h}\)、\(W_{hx} \in \mathcal{R}^{d_h \times d_i}\) 和 \(W_{yh} \in \mathcal{R}^{d_o \times d_h}\)，偏置项为 \(b_h \in \mathcal{R}^{d_h}\) 和 \(b_y \in \mathcal{R}^{d_o}\)。在时刻 \(t\)，模型的输入包含当前输入 \(x_t\) 和前一时刻的隐藏状态 \(h_{t-1}\)。这种设计使得历史信息能够逐步传递至当前时刻，从而对隐藏状态进行更新得到 \(h_t\)。更新后的隐藏状态 \(h_t\) 可以看作是历史信息的加总，对其进行非线性变化后得到当前时刻的输出 \(y_t\)。

RNNs中的单元结构

\(\hspace{1.5em}\) RNNs中的单元结构（Cell）类似于一个只接收单个训练样本的多层感知机（MLP），并且每一个时刻的MLP使用 相同的权重矩阵 （参数共享）。与普通MLP的不同之处在于，RNNs拥有反馈循环，这使得信息可以在时间序列中得以传递和保留。针对RNN单元的前向传播和反向传播，可以参考第一章（单一隐藏层神经网络--基于一个样本点）的内容。

\(\hspace{1.5em}\) 为了让大家更清楚的理解Vanilla RNN的工作原理，我们可以动手写一个 RNN Cell 类 2在 RNN Cell 中，我们只需要考虑隐藏状态 \(h_t\) 的更新，而不需要考虑输出 \(y_t\) 的计算。：

 1   import torch
 2   import torch.nn as nn
 3
 4   class RNN_Cell(nn.Module):
 5      def __init__(self, input_size, hidden_size):
 6         super(RNN_Cell, self).__init__()
 7         self.hidden_size = hidden_size
 8         self.input_size = input_size
 9         # h_t = \tanh(W_{hh} h_{t-1} + W_{{hx}} x_t + b_h)
10         # nn.Linear中包括了W_{hh}, W_{{hx}}和b_h
11         self.i2h = nn.Linear(input_size + hidden_size, hidden_size)
12
13      # input是一个时间步的输入: [input_size]
14      def forward(self, input, hidden):
15         if hidden is None:
16            hidden = torch.zeros(self.hidden_size)
17         # Cell里的input只是一个时间步的输入
18         # 将输入x_t和隐藏状态h_{t-1}拼接在一起
19         combined = torch.cat((input, hidden), 1)
20         # 得到h_t
21         hidden = self.i2h(combined)
22         return hidden

\(\hspace{1.5em}\) 在 RNN Cell 类中，我们定义了每一个时间步下，如何更新隐藏状态。而在 RNN 类中，我们需要对每一个时间步都调用 RNN Cell 类来更新隐藏状态。下面是一个简单的 RNN 类的实现：

 1   import torch
 2   import torch.nn as nn
 3   class RNN(nn.Module):
 4      def __init__(self, input_size, hidden_size, output_size):
 5         super(RNN, self).__init__()
 6         self.hidden_size = hidden_size
 7         self.rnn = RNN_Cell(input_size, hidden_size)
 8         self.output = nn.Linear(hidden_size, output_size)
 9
10      # input是整个序列: [seq_len, input_size]
11      def forward(self, input, hidden):
12         # 初始化隐藏状态
13         if hidden is None:
14            hidden = torch.zeros(self.hidden_size)
15         # 对于RNN来说，时间步等于序列长度
16         for i in range(input.size(0)):
17            # 对每一个时间步，使用RNN_Cell更新隐藏状态
18            # h_i = RNN_Cell(x_i, h_{i-1})
19            # python语法中，hidden会被更新
20            hidden = self.rnn(input[i], hidden)
21         # 得到最终的隐藏状态，通过全连接层得到输出
22         y_t = self.output(hidden)
23         return y_t

\(\hspace{1.5em}\) 通过将每一步计算隐藏状态的过程封装在 RNN Cell 类中，我们可以更清晰地理解RNN的工作原理。对于其他类型的 RNN（如 LSTM 和 GRU），唯一的区别在于 Cell 类的具体结构，而整个 RNN 类的框架是相似的 3RNN Cell 仅返回当前时间步 \(t\) 的隐藏状态，因此在 RNN 中只需处理这个状态。然而，对于即将介绍的 LSTM Cell，不仅会返回隐藏状态，还会返回一个单元状态（Cell state），因此在 LSTM 中需要同时考虑这两个状态。除此之外，RNN 和 LSTM 的基本框架几乎相同。。

如何使用循环神经网络对序列数据建模？#

\(\hspace{1.5em}\) 在循环神经网络中，每个时刻 \(t\) 我们会输入一个 \(x_t\)，对应会得到一个更新后的隐藏状态 \(h_t\) 和输出 \(\hat y_t\)。根据目标任务的不同，我们会有不同的架构（architecture）用于计算损失函数、训练模型。下面我们介绍3种架构：

  1. 堆叠架构（stacked architecture）：顾名思义，是将多个RNN堆叠在一起。在堆叠架构中，每一层的隐藏状态都会作为下一层的输入。这种架构可以帮助模型更好地捕捉序列数据中的复杂关系，提高模型的表达能力。下图展示了堆叠架构的示意图：

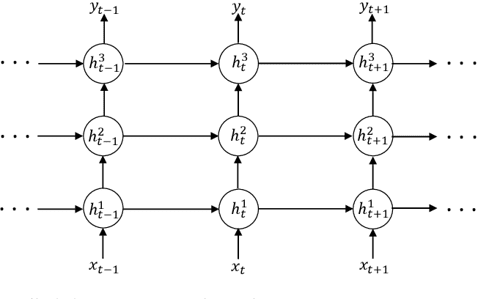
../_images/Figure_6_4_stack.png

堆叠架构的示意图#

    4在文本分析中，双向RNN能有效利用上下文信息。其中，上文信息通过正向RNN传递，下文信息通过反向RNN传递。这种架构能够更好地捕捉文本中的语义关系。

  1. 双向架构（bidirectional architecture）：在双向架构中，我们会有两个RNN，一个是正向RNN，一个是反向RNN。正向RNN会接收输入序列，然后从左到右计算隐藏状态；反向RNN会接收输入序列，然后从右到左计算隐藏状态。最后，我们会将两个RNN的隐藏状态拼接（concatenate）在一起，然后通过一个全连接层来计算输出。这种架构在序列标注、情感分析等任务中非常有效 4在文本分析中，双向RNN能有效利用上下文信息。其中，上文信息通过正向RNN传递，下文信息通过反向RNN传递。这种架构能够更好地捕捉文本中的语义关系。。下图展示了双向架构的示意图：

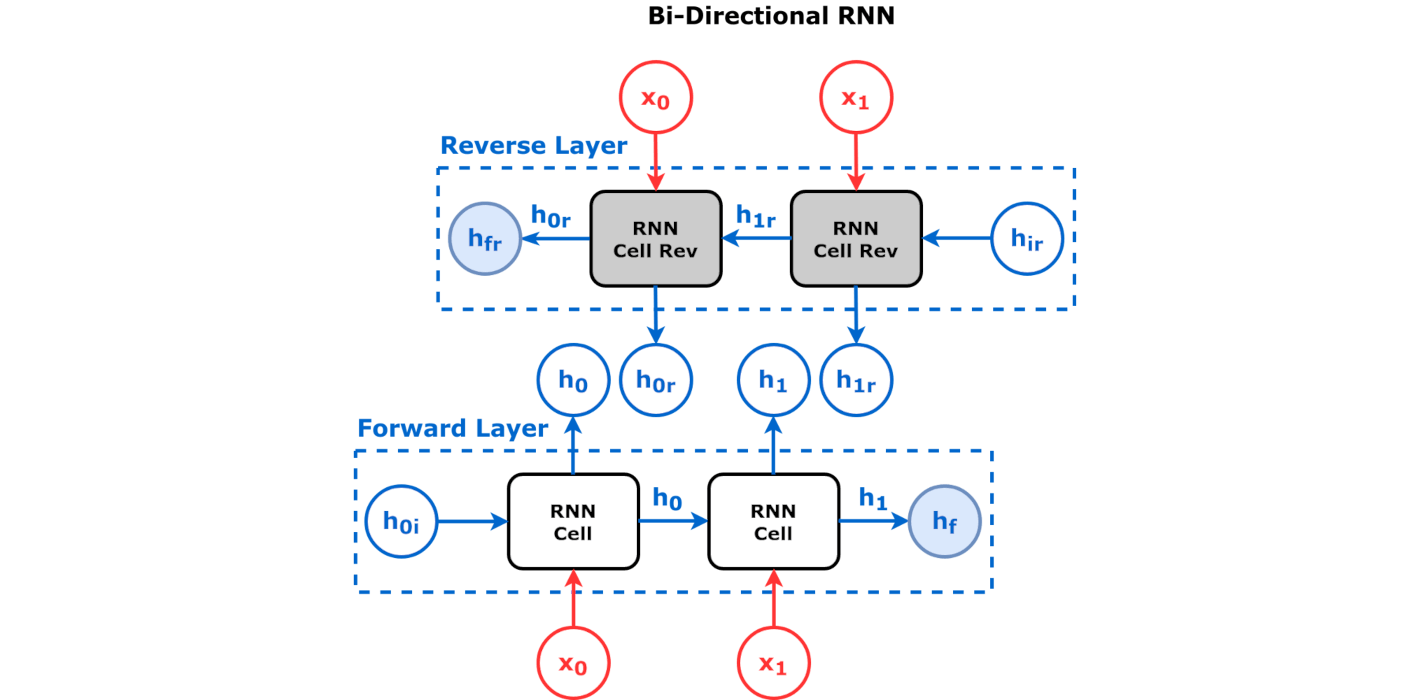
../_images/Figure_6_5_Bidirectional_RNN.png

双向RNN的示意图（图片来源： Wikipedia）#

  1. 序列到序列（seq2seq）：我们会有两个RNN，一个是编码器（encoder），一个是解码器（decoder）。编码器会接收输入序列，然后将序列的信息编码到一个固定长度的向量中，该向量可以看作是对整个序列的压缩。解码器会接收编码器的输出，然后根据这个输出来生成目标序列。这种架构在机器翻译、文本摘要等任务中非常有效。下图展示了seq2seq架构的示意图：

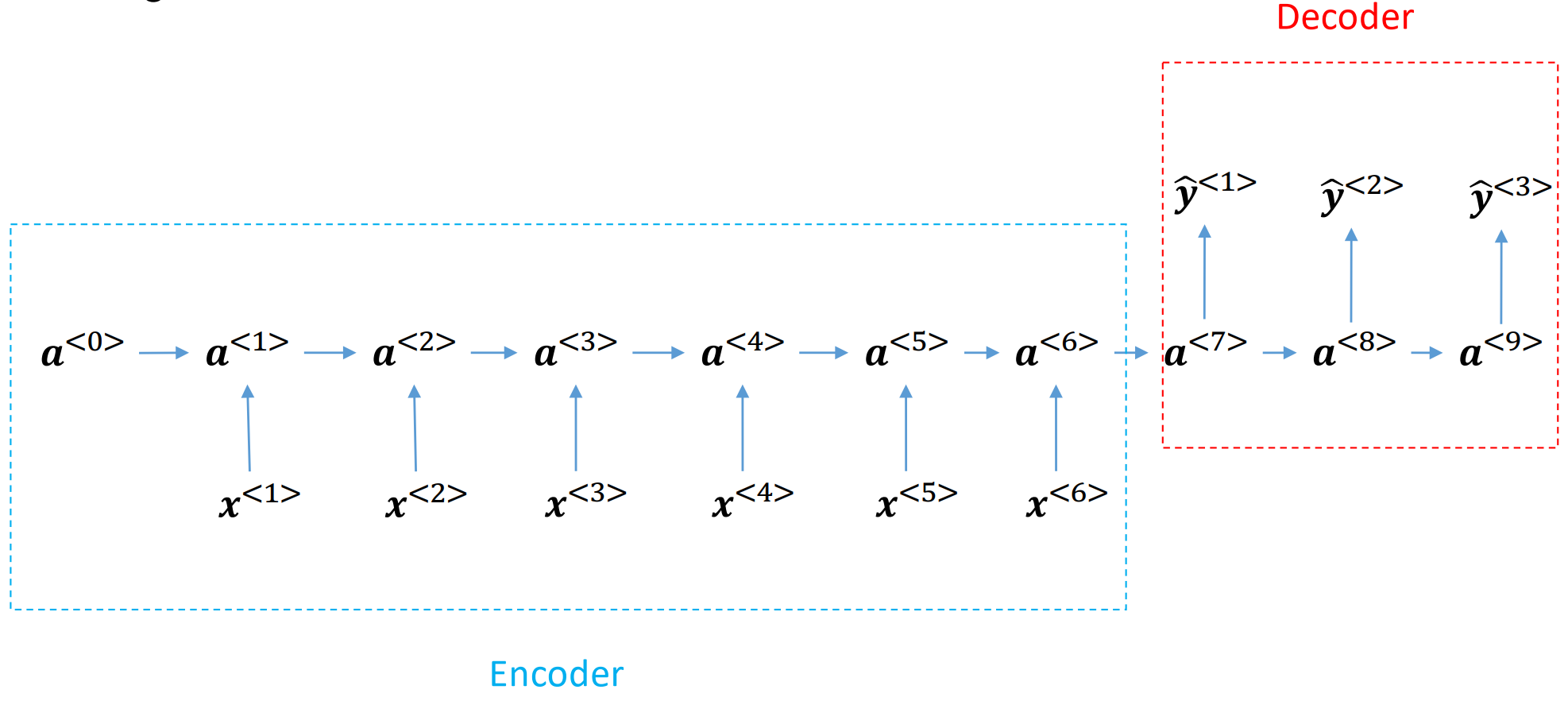
../_images/Figure_6_6_seq2seq.png

seq2seq架构的示意图#

实际应用中如何选择模型架构

\(\hspace{1.5em}\) 在实际应用中，堆叠式架构因其层级设计与时间序列中的自回归模型类似，常被用于时间序列预测。这种架构通过多层网络逐步提炼特征，能够捕捉复杂的时间依赖关系，从而提升预测性能。

\(\hspace{1.5em}\) 此外，双向架构和seq2seq架构在文本和语音分析中尤为常见。双向架构通过同时考虑前后文信息，生成更加全面的特征表示，因此在自然语言处理（NLP）任务（如命名实体识别、机器翻译和语音识别）中表现出色seq2seq架构则以其灵活性成为机器翻译、文本摘要和问答系统等任务的核心方法。在seq2seq架构中，编码器和解码器的设计可以根据任务需求灵活调整。例如，编码器可以采用双向架构以充分捕捉输入序列的上下文信息，解码器则可以使用传统的单向架构或更复杂的模型（如 Transformer），以增强对长距离依赖的处理能力。此外，还可以结合其他模型（如卷积神经网络或预训练语言模型）来进一步提升性能。这种灵活的模块化设计使seq2seq架构在适配不同应用场景时，能够保持较高的性能和泛化能力。

\(\hspace{1.5em}\) 下面，我们以模拟生成的自回归AR(1)过程为例，举例说明如何用RNN对序列数据进行建模（in-sample fitting）。

 1import torch
 2import torch.nn as nn
 3import numpy as np
 4import matplotlib.pyplot as plt
 5
 6# 模拟生成AR(1)过程
 7def generate_AR1_data(n, phi):
 8   x = np.zeros(n)
 9   for i in range(1, n):
10      x[i] = phi * x[i-1] + np.random.normal(0, 1)
11   return x
12
13# 生成数据
14n = 1000
15phi = 0.8
16x = generate_AR1_data(n, phi)
17
18# 数据预处理
19x = torch.tensor(x, dtype=torch.float32).view(-1, 1)
20# 在时间序列预测中，y_t = x_{t+1}
21# 所以我们的输入是 x_0, x_1, ..., x_998
22# 我们的输出（target）是 x_1, x_2, ..., x_999
23y = x[1:]
24x = x[:-1]
25
26# 定义RNN模型
27class RNN(nn.Module):
28   def __init__(self, input_size, hidden_size, output_size):
29      super(RNN, self).__init__()
30      self.hidden_size = hidden_size
31      # 使用torch中的RNN，这里也可以换成之前我们自己写的RNN类
32      # 后面我们会看到，这里我们还可以使用nn.LSTM或者nn.GRU
33      # bidirectional=False表示单向RNN，为True时表示双向RNN
34      # num_layers=1表示RNN的层数为1，对应stacked architecture中的层数
35      self.rnn = nn.RNN(input_size, hidden_size, num_layers=1, bidirectional=False, batch_first=True)
36      self.output = nn.Linear(hidden_size, output_size)
37
38   def forward(self, x, hidden):
39      # 请查阅pytorch官方文档，弄明白nn.RNN的输出是什么，有什么参数
40      y, hidden = self.rnn(x, hidden)
41      # 输出层
42      y = self.output(y)
43      return y, hidden
44
45# 训练模型
46input_size = 1
47hidden_size = 32
48output_size = 1
49model = RNN(input_size, hidden_size, output_size)
50criterion = nn.MSELoss()
51optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
52
53model.train()
54for epoch in range(100):
55   hidden = None
56   optimizer.zero_grad()
57   y_pred, hidden = model(x.view(1, -1, 1), hidden)
58   loss = criterion(y_pred.view(-1), y.view(-1))
59   loss.backward()
60   optimizer.step()
61
62# 预测
63model.eval()
64hidden = None
65y_pred, _ = model(x.view(1, -1, 1), hidden)
66
67# 可视化
68plt.plot(y.detach().numpy(), label='True')
69# detach是将y_pred从计算图中分离出来，不再计算梯度
70plt.plot(y_pred.detach().numpy().flatten(), label='Predicted')
71plt.legend()
72plt.show()

\(\hspace{1.5em}\) 最后模型输出如下图片 5在本例中，我们将所有数据都当作了训练数据，因此模型会出现过拟合（overfitting）的问题。在实际应用中，我们需要将数据分为训练集（参数估计，in-sample fitting）、验证集（选择额超参数，hyper-parameters tuning）和测试集（样本外预测，out-sample forecasting），以便评估模型的泛化能力。：

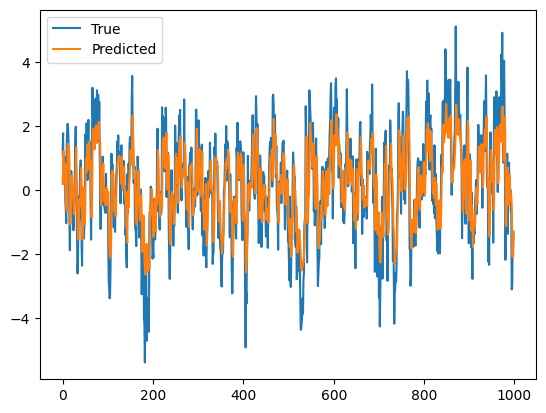
../_images/Figure_6_7_AR_predict.png

使用RNN对AR(1)过程进行预测#

随时间反向传播（backpropagation through time, BPTT）#

\(\hspace{1.5em}\) 为了研究梯度在RNN中是如何传播的，我们考虑一个简单的RNN模型。忽略激活函数和误差项 6为了更清楚直观的解释BPTT的原理，不失一般性地，我们假设激活函数为 identity 函数，即 \(\sigma(x) = x\)，偏置项为0。针对更一般的激活函数（如 \(tanh(\cdot)\) 等），只需在反向传播过程中乘上一项激活函数的导数即可。，我们可以将RNN的前向传播过程表示如下：

()#\[\begin{split}h_0 &= 0 \\ h_1 &= W_{hh} h_0 + W_{hx} x_1, \hat y_1 = W_{yh} h_1 \\ h_2 &= W_{hh} h_1 + W_{hx} x_2, \hat y_2 = W_{yh} h_2 \\ h_3 &= W_{hh} h_2 + W_{hx} x_3, \hat y_3 = W_{yh} h_3 \\ &\dots \\ h_T &= W_{hh} h_{T-1} + W_{hx} x_T, \hat y_T = W_{yh} h_T,\end{split}\]

其中，\(W_{hh}\) 、\(W_{hx}\) 、\(W_{yh}\) 是权重矩阵，也是我们需要训练的参数。为了使用梯度下降法来训练RNN，我们需要计算损失函数对权重矩阵的梯度。以均方误差作为损失函数（loss function），我们可以得到：

\[\mathcal{J} = \frac{1}{T} \sum_{t=1}^{T} (y_t - \hat y_t)^2,\]

其中，\(\mathcal{J}\) 是损失函数（cost function），\(T\) 是序列的长度。为了更新权重矩阵，我们需要计算 \(\frac{\partial \mathcal{J}}{\partial W_{hh}}\)、\(\frac{\partial \mathcal{J}}{\partial W_{hx}}\) 和 \(\frac{\partial \mathcal{J}}{\partial W_{yh}}\)。首先，我们给出一个简单的前向传播的示意图，并逐步分析RNN如何通过链式法则计算梯度：

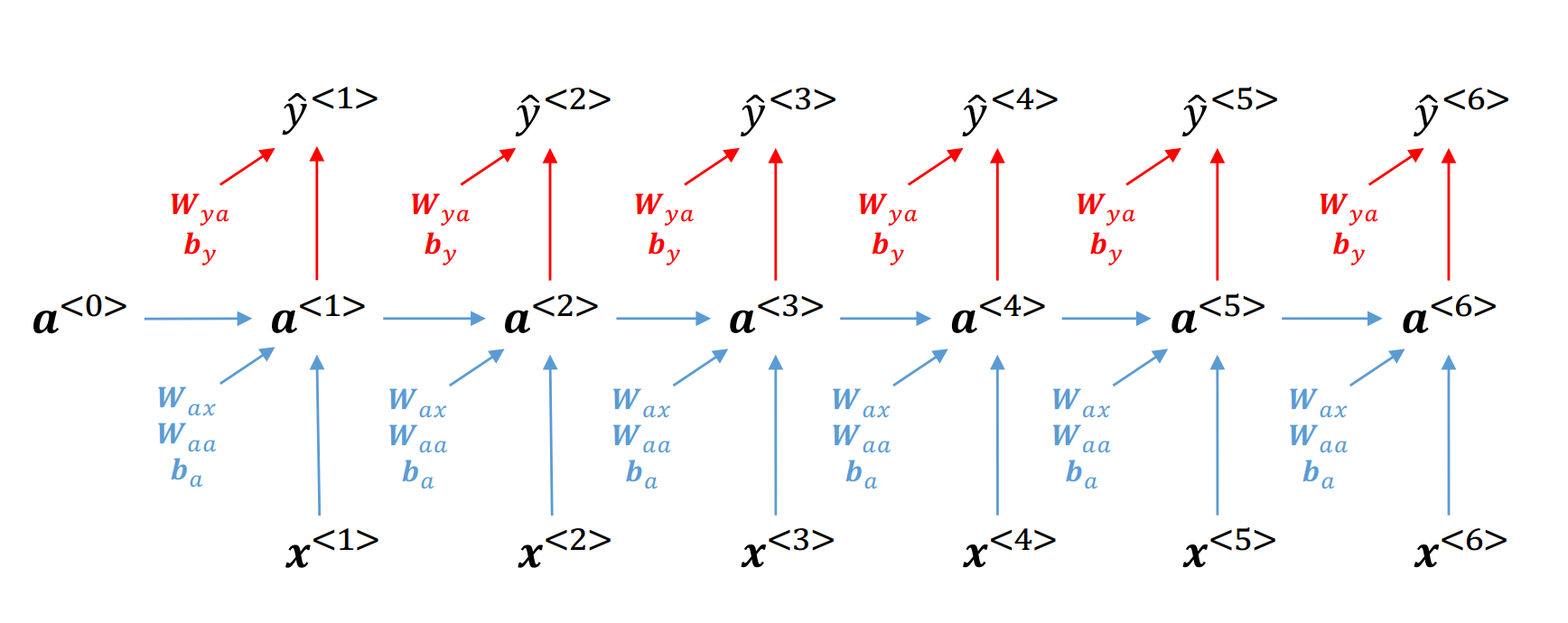
../_images/Figure_6_8_RNN_forward.png

RNN的前向传播示意图#

\(\hspace{1.5em}\) 对于 \(W_{yh}\)，我们可以发现每个时刻 \(t\) 都存在一条 \(\mathcal{J} \to \hat y_t \to W_{yh}\) 的路径。因此，我们可以直接计算梯度：

\[\begin{split}\frac{\partial \mathcal{J}}{\partial W_{yh}} &= \sum_{t=1}^{T} \frac{\partial \mathcal{J}}{\partial \hat y_t} \frac{\partial \hat y_t}{\partial W_{yh}} \\ &= \sum_{t=1}^{T} - \frac{2}{T} (y_t - \hat y_t) (h_t)^{\top}.\end{split}\]

\(\hspace{1.5em}\) 对于 \(W_{hh}\) 和 \(W_{hx}\)，在计算梯度时我们需要考虑未来时刻的梯度如何反向传播到当前时刻。在上图中，以时刻 \(3\) 的 \(W_{hh}\) 为例，会有多条路径从 \(\mathcal{J}\) 到 \(W_{hh}\)。这些路径包括：

()#\[\begin{split}\mathcal{J} \to \hat y_3 \to h_3 &\to W_{hh} \\ \mathcal{J} \to \hat y_4 \to h_4 \to h_3 &\to W_{hh} \\ \mathcal{J} \to \hat y_5 \to h_5 \to h_4 \to h_3 &\to W_{hh} \\ \mathcal{J} \to \hat y_{6} \to h_{6} \to \dots \to h_3 &\to W_{hh}.\end{split}\]

\(\hspace{1.5em}\) 为了简化计算，我们考虑如下简化的路径：\(\mathcal{J} \to (\cdot) \to h_t \to W_{hx}/W_{yh}\)，其中 \((\cdot)\) 代表了所有可能的路径。因此，我们可以将链式法则表示为：

\[\begin{split}\frac{\partial \mathcal{J}}{\partial W_{hh}} &= \sum_{i=1}^{T} \frac{\partial \mathcal{J}}{\partial \hat h_{i}} \frac{\partial \hat h_{i}}{\partial W_{hh}} \\ \frac{\partial \mathcal{J}}{\partial W_{hx}} &= \sum_{i=1}^{T} \frac{\partial \mathcal{J}}{\partial \hat h_{i}} \frac{\partial \hat h_{i}}{\partial W_{hx}}.\end{split}\]

\(\hspace{1.5em}\) 这样做的好处在于，路径 \(h_t \to W_{hx}/W_{hh}\) 的梯度是容易算的，我们只需要弄清楚 \(\mathcal{J} \to (\cdot) \to h_t\) 这一部分的梯度即可。由 () 我们可以推出时刻 \(t\) 时 \(\mathcal{J} \to (\cdot) \to h_t\) 可以取以下路径：

\[\begin{split}\mathcal{J}& \to \hat y_t & \to h_t \\ \mathcal{J}& \to \hat y_{t+1} \to h_{t+1} & \to h_t \\ \mathcal{J}& \to \hat y_{t+2} \to h_{t+2} \to h_{t+1} & \to h_t \\ &\vdots \\ \mathcal{J}& \to \hat y_{T} \to h_{T} \to \dots \to h_{t+1} & \to h_t.\end{split}\]

\(\hspace{1.5em}\) 因此，在计算 \(\frac{\partial \mathcal{J}}{\partial h_t}\) 时，我们会得到如下结果：

()#\[\begin{split}\frac{\partial \mathcal{J}}{\partial h_t} &= \sum_{\tau = t}^{T} \frac{\partial \mathcal{J}}{\partial \hat y_{\tau}} \frac{\partial \hat y_{\tau}}{\partial h_{\tau}} (\Pi_{i=t+1}^{\tau} \frac{\partial h_{i}}{\partial h_{i-1}}) \\ &= - \frac{2}{T} \sum_{\tau = t}^{T} {\color{red}{(W_{hh}^{\top})^{\tau - t}}} W_{yh}^{\top} (y_{T + t - \tau} - \hat y_{T + t - \tau}).\end{split}\]

RNN中的梯度消失/爆炸

\(\hspace{1.5em}\) 由 () 我们可以看到，从 \(\mathcal{J} \to \hat y_{\tau} \to h_{\tau} \to \dots \to h_{t+1} \to h_t\) 这条路径反向传播的梯度，梯度的大小与 \((W_{hh}^{\top})^{\tau - t}\) 有关。当 \(\tau \gg t\) 时，如果 \(\|W_{hh}\| > 1\)，梯度会出现NaN（梯度爆炸），导致模型参数无法更新；如果 \(\|W_{hh}\| < 1\)，梯度会趋于0（梯度消失）。因为有多条路径反向传播，在梯度消失时，近距离的梯度成为主项（dominant），因此模型无法利用远距离（\(\tau \gg t\)）的梯度。此时，在每一个时刻 \(t\)，模型只能学习到近距离的信息，而无法学习长距离的依赖关系（long-term dependence）。

\(\hspace{1.5em}\) 最后，应用链式法则，我们可以得到：

\[ \begin{align}\begin{aligned}\begin{split}\frac{\partial \mathcal{J}}{\partial W_{hh}} &= \sum_{t = 1}^{T} \frac{\partial \mathcal{J}}{\partial h_t} \frac{\partial \hat h_{i}}{\partial W_{hh}} \\ &= \sum_{t = 1}^{T} \frac{\partial \mathcal{J}}{\partial h_t} (h_{t-1})^{\top}\end{split}\\\begin{split}\frac{\partial \mathcal{J}}{\partial W_{hx}} &= \sum_{t = 1}^{T} \frac{\partial \mathcal{J}}{\partial h_t} \frac{\partial \hat h_{i}}{\partial W_{hx}} \\ &= \sum_{t = 1}^{T} \frac{\partial \mathcal{J}}{\partial h_t} (x_{t})^{\top},\end{split}\end{aligned}\end{align} \]

其中 \(\frac{\partial \mathcal{J}}{\partial h_t}\) 由 () 给出。

BPTT的计算

\(\hspace{1.5em}\) 在上述计算中，我们显示的将所有可能的路径写出来然后进行梯度的计算。在实际应用中，我们可以递归的计算梯度 \(\frac{\partial \mathcal{J}}{\partial h_t}\)，这样既简洁又高效。下面我们简要说明一下如何计算。

\(\hspace{1.5em}\) 当 \(t = T\) （最后一步）时，只有一条路径反向传播梯度：

  1. \(\mathcal{J} \to \hat y_T \to h_T\)；

\[\frac{\partial \mathcal{J}}{\partial h_T} = \frac{\partial \mathcal{J}}{\partial \hat y_T} \frac{\partial \hat y_T}{\partial h_{T}}.\]

在时刻 \(t < T\) 时，梯度经过两条路径反向传播：

  1. \(\mathcal{J} \to \hat y_t \to h_t\)；

  2. \(\mathcal{J} \to \dots \to h_{t+1} \to h_t\)。

\[\frac{\partial \mathcal{J}}{\partial h_t} = \frac{\partial \mathcal{J}}{\partial h_{t+1}} \frac{\partial h_{t+1}}{\partial h_{t}} + \frac{\partial \mathcal{J}}{\partial \hat y_t} \frac{\partial \hat y_t}{\partial h_{t}}.\]

\(\hspace{1.5em}\) 利用上述的两个公式，我们便可以递归的计算 \(\frac{\partial \mathcal{J}}{\partial h_t}\)。