卷积神经网络#
\(\hspace{1.5em}\) 在上一节中,我们介绍了卷积的基本概念。在本节中,我们将介绍卷积神经网络(Convolutional Neural Network, CNN)的基本结构。一个基本的卷积神经网络通常包括若干个卷积层、池化层和全连接层。卷积层用于提取输入数据的特征,池化层用于减小输出维度,全连接层用于整合卷积层提取的特征。
卷积层#
\(\hspace{1.5em}\) 卷积层是卷积神经网络的核心部分。与全连接层不同,卷积层对输入数据的每个局部区域进行卷积运算并加上偏置,然后通过激活函数进行非线性变换后得到输出。考虑大小为 \(d_H\times d_W\) 的输入“图像” \(\bX=(x_{ij})\) ,以及大小为 \(f\times f\) 的卷积核 \(\bW=(w_{kl})\) 。我们令 Stride 为1, Padding 为0,卷积层的计算公式如下:
其中 \(\bZ=(z_{ij})\) 为卷积计算结果,\(\sigma\) 是激活函数,\(b\) 是偏置,括号中的第一项是上节所介绍的卷积运算。需要指出的是,在得到卷积结果 \(\bZ\) 时,我们运用的是一个公共的偏置。用矩阵表示,卷积层的计算公式如下:
其中 \(\ast\) 表示卷积运算,\(\boldsymbol{W}\) 是卷积核。在 () 中,我们运用了 NumPy 的 广播机制 进行关于偏置的计算。
计算卷积层的参数包括卷积核和偏置,因此卷积层的参数数量为 \(f\times f + 1\) 。这个参数量级与输入图像的维度并无直接关系。对比与全连接神经网络模型,当输入图像规模很大时,卷积层的参数数量远小于全连接层的参数数量。
\(\hspace{1.5em}\) 与一层全连接层有多个神经元类似,一个卷积层通常也包含多个卷积核,分别提取图像的不同信息。需要指出的是,每个卷积核对应着一个偏置项。每个卷积核对输入数据进行卷积运算,然后通过激活函数进行非线性变换后得到输出。在下图中,我们运用 \(K\) 个卷积核进行信息提取:

\(\hspace{1.5em}\) 下面这个视频演示了多个卷积核同时对一个输入进行卷积,提取不同特征的过程:
\(\hspace{1.5em}\) 回到本章开头的问题,卷积层的两个重要性质充分减少了参数数量,并且使得卷积神经网络对平移具有不变性。这两个性质分别是:
局部连接:卷积层计算结果中的每个值只与输入图像数据的一个局部区域相连,因此我们可以通过一个维度小得多的卷积核来替代全连接层的大型权重矩阵。
参数共享:卷积层计算结果对于输入数据的每个局部区域使用相同的卷积核,减少了参数数量。此外,由于所有局部区域使用的是相同的卷积核,因此无论目标对象在图像中的位置如何,卷积层都可以有效的提取出目标对象的特征。
\(\hspace{1.5em}\) 但是,尽管卷积层的参数数量大大减少,卷积层的输出维度仍然可能很大。具体地讲,对于大小为 \(d_H\times d_W\) 的输入数据,大小为 \(f\times f\) 的卷积核, Stride 为 \(s\) , Padding 为 \(p\) ,卷积层的输出维度为:
其中 \(\lfloor\cdot\rfloor\) 表示向下取整。由于通常卷积核的维度以及 Stride 的大小并不会很大,因此卷积层的输出维度仍然保持在一个相当大的规模。如果在卷积层之后直接连接全连接层,全连接层的参数数量将会非常庞大,容易导致过拟合。因此,我们通常会在卷积层之后添加池化层来减小输出维度。
下采样
\(\hspace{1.5em}\) 一般将减小维度的操作称为“下采样”,而将增加维度的操作称为“上采样”。设置池化层、增加 Stride 等操作都可以减小输出维度,因此都可以看作是下采样操作。
池化层#
\(\hspace{1.5em}\) 池化层(Pooling Layer)是卷积神经网络的另一个重要组成部分。池化层的作用是通过对输入数据的局部区域进行池化操作,减小输出维度。假设输入池化层的数据为 \(\bX\) ,大小为 \(d_H\times d_W\) ,可以将输入数据划分为若干个大小为 \(f\times f\) 的局部区域,这些局部区域之间允许有重叠。请注意,与卷积核类似,此处我们仍然用 \(f\) 表示局部区域大小。池化操作是对每个局部区域的数值进行某种统计操作,例如最大值、平均值等。常见的池化操作是最大池化(Max Pooling)和平均池化(Average Pooling)。对应于池化过程,我们通常令 Stride 为 \(s=f\),Padding 为 \(p=0\)。记输出结果为 \(\bZ=(z_{ij})\),其规模可通过 () 计算得到。下面我们讲介绍两种池化的计算过程。
\(\hspace{1.5em}\) 最大池化是对每个局部区域取最大值,计算公式如下:
\(\hspace{1.5em}\) 平均池化是对每个局部区域取平均值,计算公式如下:
\(\hspace{1.5em}\) 下面这个视频展示了最大池化和平均池化的过程:
\(\hspace{1.5em}\) 池化层的参数数量为0,因此池化层不会增加模型的参数数量。池化层的主要作用是减小输出维度,从而减少全连接层的参数数量,防止过拟合。另外,池化层是对每个局部区域的特征进行某种程度的不变性操作,使得模型对于输入数据的微小变化具有稳健性。同时,池化层也是对局部区域特征的浓缩,使得模型更加关注图像的全局特征。
卷积神经网络的基本结构#
\(\hspace{1.5em}\) 一个最典型的卷积神经网络通常包括若干个卷积层、池化层和全连接层。卷积神经网络的结构通常如下:
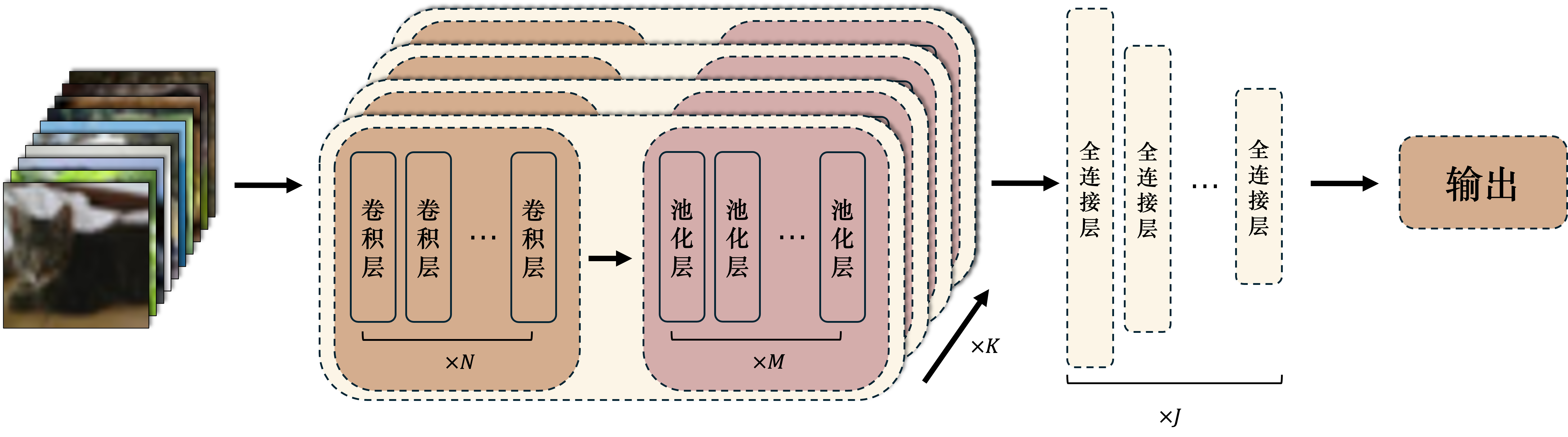 1注意与上文多个卷积核同时对一个输入进行卷积不同,这里的卷积层是顺序排列的,每个卷积层的输出作为下一个卷积层的输入。
1注意与上文多个卷积核同时对一个输入进行卷积不同,这里的卷积层是顺序排列的,每个卷积层的输出作为下一个卷积层的输入。卷积神经网络的基本结构1注意与上文多个卷积核同时对一个输入进行卷积不同,这里的卷积层是顺序排列的,每个卷积层的输出作为下一个卷积层的输入。。#
卷积模块:卷积模块由若干个卷积层和池化层组成。卷积层用于提取输入数据的特征,池化层用于减小输出维度。卷积模块的输出是一个高维特征图,包含了输入数据的局部特征。一般的卷积神经网络会包含多个卷积模块,每个卷积模块的输出作为下一个卷积模块的输入。
全连接模块:全连接模块由若干个全连接层组成。全连接层一方面用于整合卷积模块提取的特征,为神经网络提供更强的非线性表达能力;另一方面,全连接层可以看作是神经网络的“记忆”模块,保存着神经网络从训练数据中学到的知识。
\(\hspace{1.5em}\) 在后面的章节中,我们会更为具体的介绍一些经典的卷积神经网络结构,例如LeNet、AlexNet、VGG、GoogLeNet、ResNet等。这些卷积神经网络结构在图像分类、目标检测、语义分割等任务中取得了非常好的效果,是深度学习领域的重要里程碑。在这之前,让我们先学习一下卷积神经网络的反向传播。